Introducción

En este capítulo se hace una comparación entre la prueba estadística no paramétrica Mann–Whitney–Wilcoxon y la prueba T.

La prueba T es un test estadístico paramétrico que permite contrastar la hipótesis nula de que las medias de dos poblaciones son iguales, frente a la hipótesis alternativa de que no lo son.

$$ \begin{equation} H_{0}: \mu_{A}=\mu_{B} \end{equation} $$ $$ \begin{equation} H_{a}: \mu_{A} \neq \mu_{B} \end{equation} $$

Otra forma equivalente de definir estas hipótesis es:

$$ \begin{equation} H_{0}: \mu_{A}-\mu_{B}=0 \end{equation} $$ $$ \begin{equation} H_{a}: \mu_{A}-\mu_{B} \neq 0 \end{equation} $$

A pesar de la sencillez y utilidad del t-test, para que sus resultados sean válidos es necesario que se cumplan una serie de condiciones, entre las que se encuentran:

• Independencia: Las observaciones tienen que ser independientes las unas de las otras. Para ello, el muestreo debe ser aleatorio y el tamaño de la muestra inferior al 10% de la población. (Existe una adaptación de t-test para datos pareados)
• Normalidad: Las poblaciones que se comparan tienen que seguir una distribución normal. Si bien la condición de normalidad recae sobre las poblaciones, no se suele disponer de información sobre ellas, por lo que se emplean las muestras (dado que son reflejo de la población) para determinarlo. En caso de cierta asimetría, los t-test son considerablemente robustos si el tamaño de las muestras es mayor o igual a 30.
• Igualdad de varianza (homocedasticidad): la varianza de las poblaciones comparadas debe de ser igual. Tal como ocurre con la condición de normalidad, si no se dispone de información de las poblaciones, esta condición se ha de asumir a partir de las muestras. En caso de no cumplirse esta condición se puede emplear un Welch Two Sample t-test, que incorpora una corrección a través de los grados de libertad que compensa la diferencia de varianzas, con el inconveniente de que pierde poder estadístico.

Para información más detallada del t-test consultar T-test.

Es importante evaluar hasta que punto, el no cumplimiento de una o varias de sus condiciones, puede afectar al resultado del t-test. Si su utilización queda descartada, se puede recurrir a otros test estadísticos.

Evaluación del t-test con distribuciones no normales para distintos tamaños muestrales

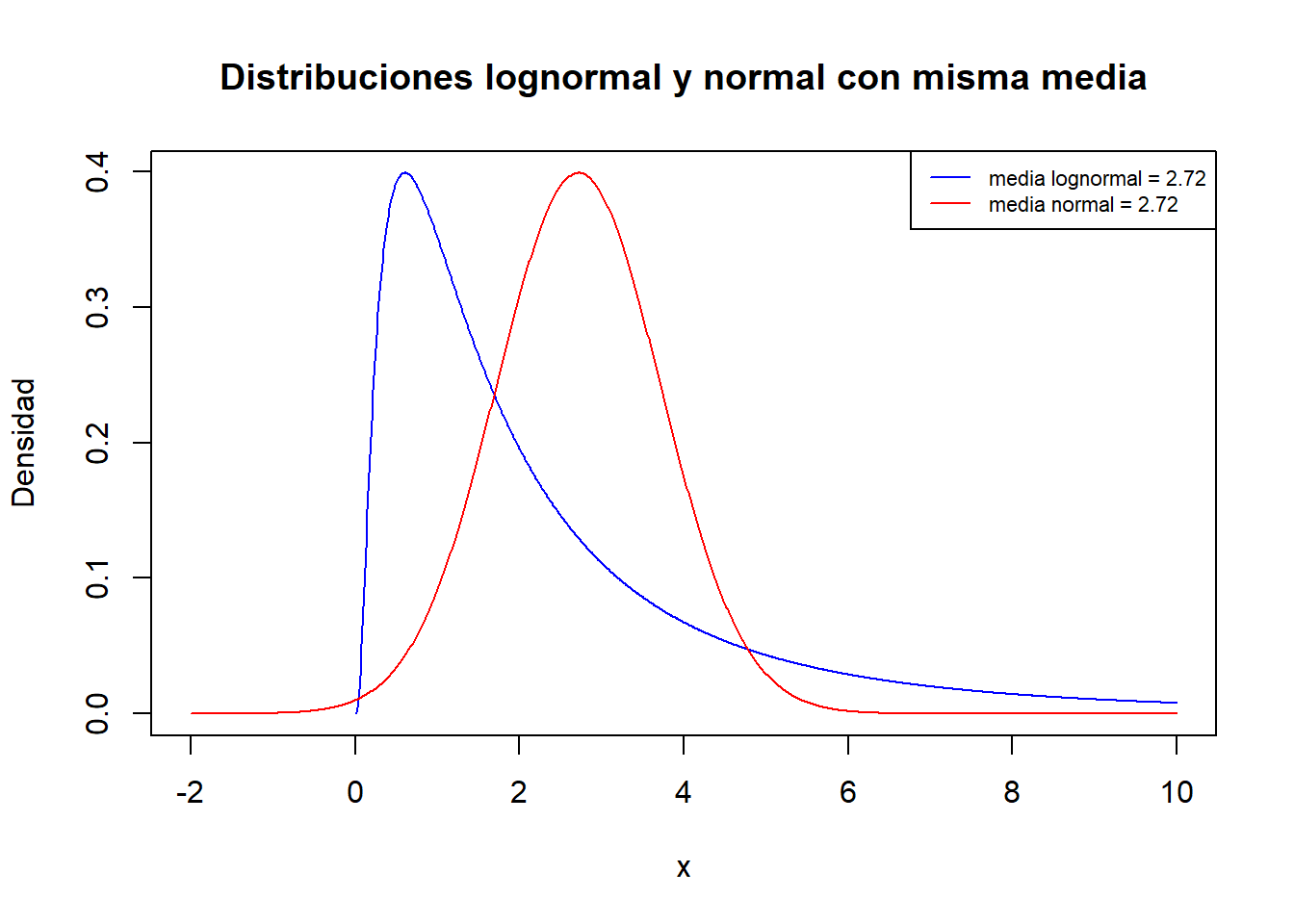
Una de las principales razones que por las que los investigadores descartan la utilización del t-test es por la falta de normalidad en la distribución de las muestras. Si bien es cierto que el t-test requiere como condición que las poblaciones de origen sigan una distribución normal, a medida que se incrementa el tamaño de las muestras se vuelve menos sensible al no cumplimiento de esta condición. En el siguiente ejemplo se simulan dos poblaciones con la misma media, una de las cuales tiene mucha asimetría, y se evalúa el resultado de un t-test para diferentes tamaños muestrales.

x <- seq(0, 10, length = 1000)
y <- dlnorm(x = x, meanlog =  0.5, sdlog = 1)
plot(x, y, type = "l", lty = 1, xlab = "x", col = "blue", ylab = "Densidad",
     main = "Distribuciones lognormal y normal con misma media",
     xlim = c(-2, 10))
x_2 <- seq(-2, 10, length = 1000)
y_2 <- dnorm(x = x_2, mean = 2.718282, sd = 1)
lines(x_2, y_2, col = "red")
legend("topright",
       legend = c("media lognormal = 2.72", "media normal = 2.72"),
       col = c("blue", "red"), lty = 1, cex = 0.7)

Output

Para los tamaños muestrales 5, 10, 20, 30, 50, 100, 200, 300, 500 se extraen 1000 observaciones y se identifica el porcentaje test que se considerarían significativos para un nivel de significancia α=0.05.

El nivel basal esperado es del 5%.

test_significativos <- vector(mode = "numeric")
tamanyo_muestral <- c(5, 10, 20, 30, 50, 100, 200, 300, 500)
for(i in tamanyo_muestral){
  p_values <- rep(NA, 1000)
  for(j in 1:1000) {
    muestra_a <- rlnorm(n = i, meanlog =  0.5, sdlog = 1)
    muestra_b <- rnorm(n = i, mean = 2.718282, sd = 1)
    p_values[j] <- t.test(muestra_a, muestra_b, var.equal = FALSE)$p.value
  }
test_significativos <- c(test_significativos, mean(p_values < 0.05)*100)
}
names(test_significativos) <- c(5, 10, 20, 30, 50, 100, 200, 300, 500)
test_significativos

   5   10   20   30   50  100  200  300  500 
13.6 12.6 11.1 10.2  7.6  6.7  6.1  6.8  6.5 

plot(x = tamanyo_muestral, y = test_significativos, type = "b", ylim = c(0,20),
     ylab = "% de test significativos", xlab = "tamaño muestral")
abline(h = 5, col = "firebrick")

Output

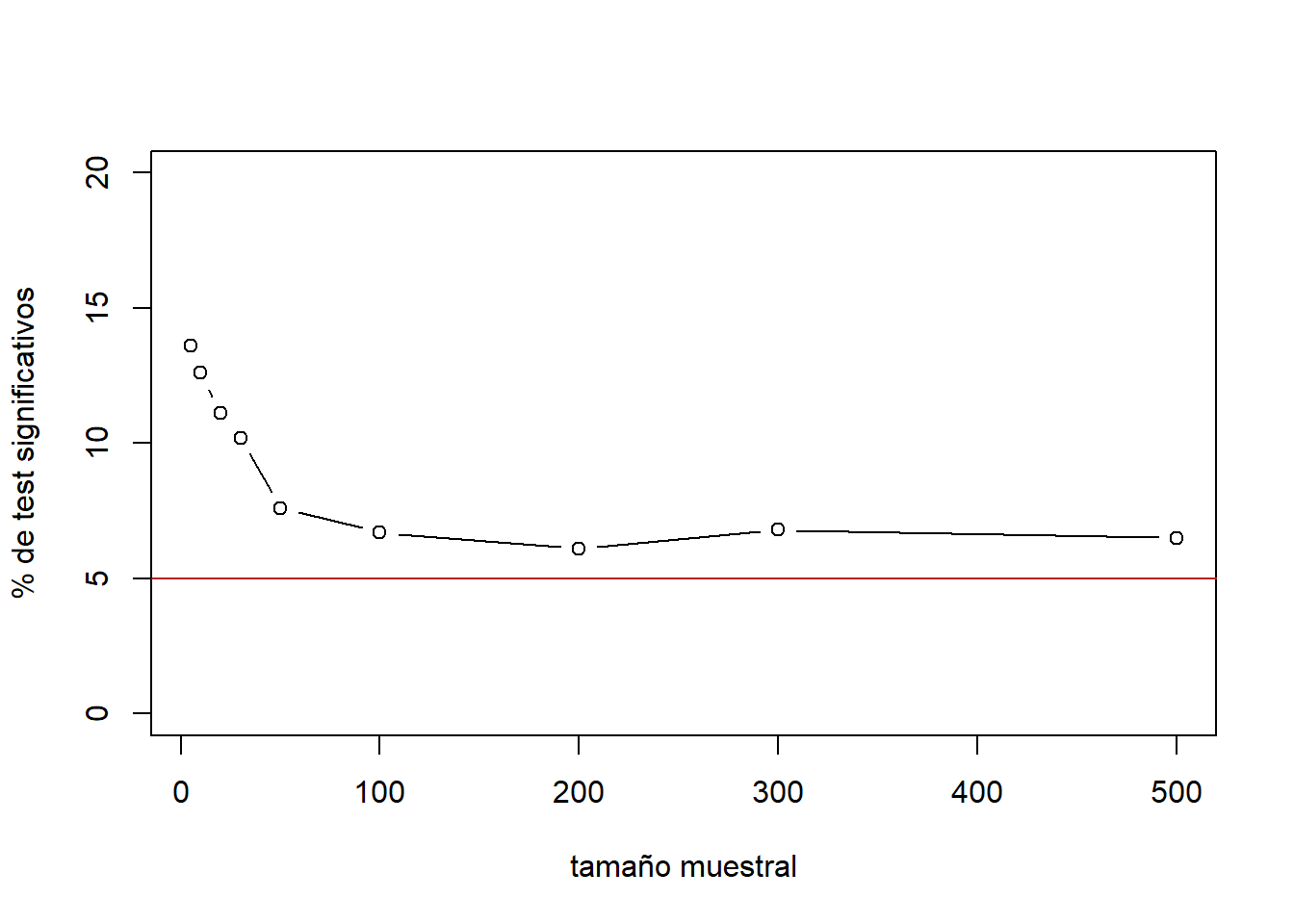
La simulación muestra que, debido a la pronunciada desviación respecto de la normalidad que presenta una de las poblaciones, para tamaños muestrales por debajo de 100 observaciones el % de test que resultan significativos está bastante por encima del nivel basal, lo que da lugar a demasiados falsos positivos. A partir de 100 observaciones, el % de test significativos se aproxima al nivel basal teórico (5%), por lo que la capacidad del t-test pasa a ser buena.

Mann Whitney Wilcoxon

El test de Mann–Whitney–Wilcoxon (WMW), también conocido como Wilcoxon rank-sum test o u-test, es un test no paramétrico que contrasta si dos muestras proceden de poblaciones equidistribuidas.

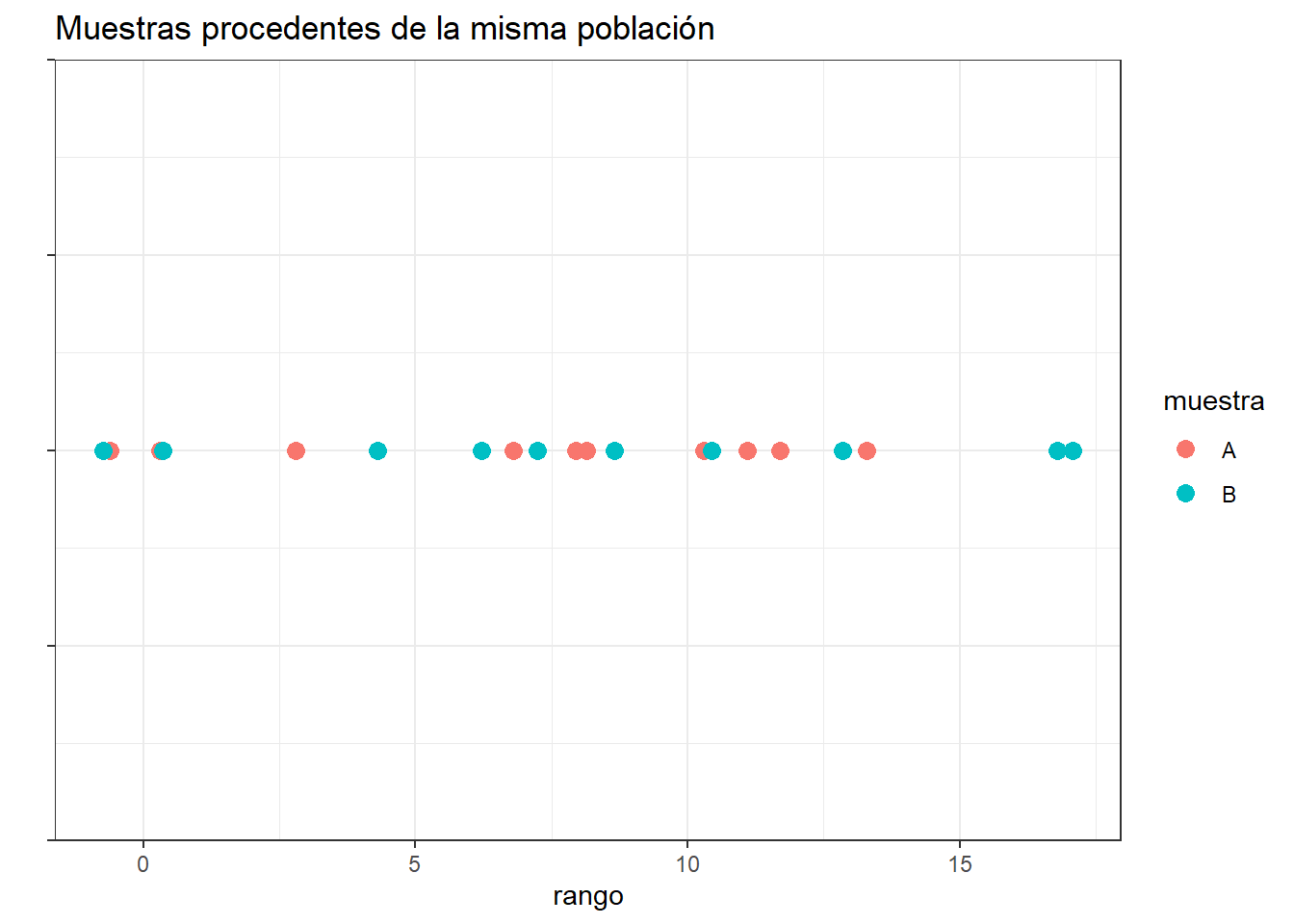
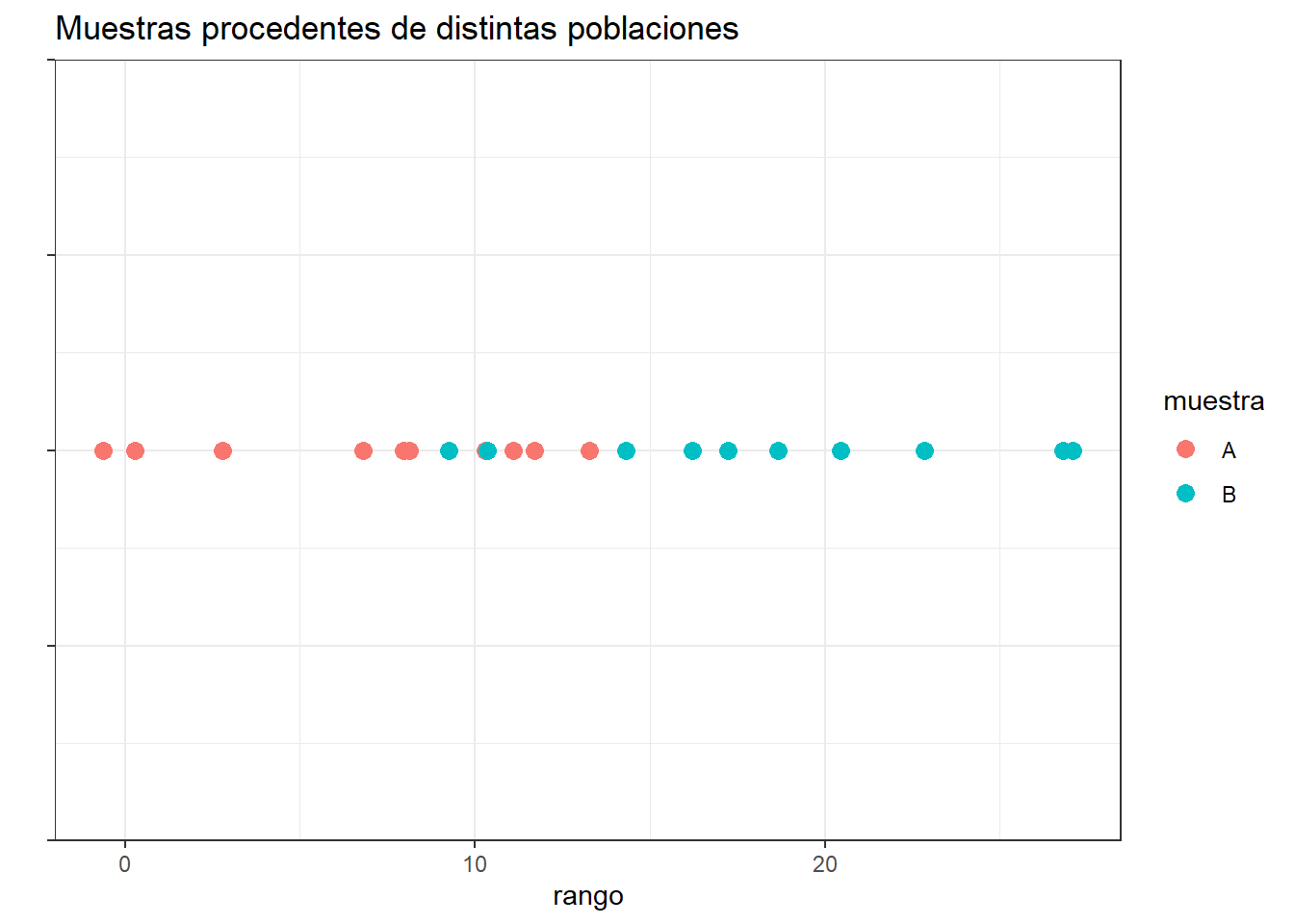
La idea en la que se fundamenta este test es la siguiente: si las dos muestras comparadas proceden de la misma población, al juntar todas las observaciones y ordenarlas de menor a mayor, cabría esperar que las observaciones de una y otra muestra estuviesen intercaladas aleatoriamente. Por lo contrario, si una de las muestras pertenece a una población con valores mayores o menores que la otra población, al ordenar las observaciones, estas tenderán a agruparse de modo que las de una muestra queden por encima de las de la otra.

library(ggplot2)
set.seed(567)
datos <- data.frame(muestra = rep(c("A", "B"), each = 10),
valor = rnorm(n = 20, mean = 10, sd = 5),
cordenada_y = rep(0, 20))

ggplot(data = datos, aes(x = valor, y = cordenada_y)) +
geom_point(aes(colour = muestra), size = 3) +
ylab("") + xlab("rango") +
theme_bw() +
theme(axis.text.y = element_blank()) + 
ggtitle("Muestras procedentes de la misma población")

Output

set.seed(567)
datos <- data.frame(muestra = rep(c("A", "B"), each = 10),
valor = c(rnorm(n = 10, mean = 10, sd = 5), rnorm(n = 10, mean = 20, sd = 5)),
cordenada_y = rep(0, 20))

ggplot(data = datos, aes(x = valor, y = cordenada_y)) +
geom_point(aes(colour = muestra), size = 3) +
ylab("") + xlab("rango") +
theme_bw() +
theme(axis.text.y = element_blank()) + 
ggtitle("Muestras procedentes de distintas poblaciones")

Output

Acorde a esta idea, el test de Mann–Whitney–Wilcoxon contrasta que la probabilidad de que una observación de la población X supere a una observación de la población Y es igual a la probabilidad de que una observación de la población Y supere a una de la población X. Es decir, que los valores de una población no tienden a ser mayores que los de otra.

$$ \begin{equation} H_{0}: P(X>Y)=P(Y>X) \end{equation} $$ $$ \begin{equation} H_{0}: P(X>Y)=0.5 \end{equation} $$ $$ \begin{equation} H_{a}: P(X>Y) \neq P(Y>X) \end{equation} $$ $$ \begin{equation} H_{a}: P(X>Y) \neq 0.5 \end{equation} $$

Es común encontrar mencionado que el test de Mann–Whitney–Wilcoxon compara medianas, sin embargo, esto solo es cierto cuando las poblaciones comparadas difieren únicamente es su localización, pero el resto de características (dispersión, asimetría…) son iguales.

Al igual que ocurre con muchos test no paramétricos, el test de Mann–Whitney–Wilcoxon es menos potente que el t-test (tienen menos probabilidad de rechazar la H0

cuando realmente es falsa) ya que ignora valores extremos. En el caso de los t-test, al trabajar con medias, si los tienen en cuenta. Esto hace a su vez que el test de Mann–Whitney–Wilcoxon sea una prueba más robusta que los t-test. En concreto, la perdida de potencia es del 5%.

Condiciones necesarias del test de Mann–Whitney–Wilcoxon

• Los datos tienen que ser independientes.
• Los datos tienen que ser ordinales o bien se tienen que poder ordenar de menor a mayor.
• No es necesario asumir que las muestras se distribuyen de forma normal o que proceden de poblaciones normales. Pero, para que el test compare medianas, ambas han de tener el mismo tipo de distribución (varianza, asimetría…).
• Igualdad de varianza entre grupos (homocedasticidad).

Ejemplo: Solución manual

Supóngase que se dispone de dos muestras, de las que no se conoce el tipo de distribución de las poblaciones de origen y cuyo tamaño es demasiado pequeño para determinar si siguen una distribución normal. ¿Existe una diferencia significativa entre poblaciones? Se emplea un ejemplo con muestras pequeñas para poder ilustrar fácilmente los pasos, no significa que con muestras tan pequeñas el test de Mann–Whitney–Wilcoxon sea preciso.

muestraX <- c( 1.1, 3.4, 4.3, 2.1, 7.0 , 2.5 )
muestraY <- c( 7.0, 8.0, 3.0, 5.0, 6.2 , 4.4 )

Al disponer de tan pocas observaciones y desconocer las poblaciones de origen, no se puede asumir que a excepción de su localización ambas distribuciones son iguales, por lo tanto, las hipótesis que contrasta el test de Mann–Whitney–Wilcoxon en este caso no se basan en medianas sino:

• \(H_{0}\): La probabilidad de que una observación de la población X sea mayor que una observación de la población Y es igual que la probabilidad de que una observación de la población Y sea mayor que una observación de la población X.

$$ \begin{equation} P(X>Y)=P(Y>X) \end{equation} $$

• \(H_{a}\): La probabilidad de que una observación de la población X sea mayor que una observación de la población Y no es igual que la probabilidad de que una observación de la población Y sea mayor que una observación de la población X.

$$ \begin{equation} P(X>Y) \neq P(Y>X) \end{equation} $$

Para poder aplicar el test de Mann–Whitney–Wilcoxon se requiere que la varianza sea igual en los dos grupos. Los test más recomendados para analizar homocedasticidad en estos casos son el test de Levene o el test de Fligner-Killeen, ambos trabajan con la mediana por lo que son menos sensibles a la falta de normalidad (si se está empleando un test de Mann–Whitney–Wilcoxon suele ser porque los datos no se distribuyen de forma normal).

fligner.test(x = list(muestraX,muestraY))

	Fligner-Killeen test of homogeneity of variances

data:  list(muestraX, muestraY)
Fligner-Killeen:med chi-squared = 0.07201, df = 1, p-value = 0.7884

No hay evidencias en contra de la igualdad de varianzas.

Una vez comprobadas las condiciones necesarias para que el test de Mann–Whitney–Wilcoxon sea válido se procede a calcular su estadístico, p-value asociado y tamaño de efecto.

Ordenación de las observaciones

Se juntan todas las observaciones, se ordenan y se les asigna un número de posición, siendo la posición 1 para el valor más pequeño. En caso de haber valores repetidos, fenómeno conocido como ligadura o ties, se les asigna como valor de posición la media de las posiciones que ocupan. En este caso, el valor “7.0” está repetido dos veces, por lo que en lugar de asignarles “10” y “11”, se les asigna “10.5” a cada uno.

# unión de las muestras y ordenación
observaciones  <- sort(c(muestraX, muestraY)) 
# La función rank() de R calcula las posiciones automáticamente,
# solucionando las ligaduras en caso de que las haya.
rango_observaciones <- rank(observaciones) 
observaciones  <- cbind(observaciones, rango_observaciones)
observaciones

      observaciones rango_observaciones
 [1,]           1.1                 1.0
 [2,]           2.1                 2.0
 [3,]           2.5                 3.0
 [4,]           3.0                 4.0
 [5,]           3.4                 5.0
 [6,]           4.3                 6.0
 [7,]           4.4                 7.0
 [8,]           5.0                 8.0
 [9,]           6.2                 9.0
[10,]           7.0                10.5
[11,]           7.0                10.5
[12,]           8.0                12.0

Cálculo del estadístico U

\(U=\min (U_{1}, U_{2})\), siendo \(U_{1}\) y \(U_{2}\) los valores estadísticos de U Mann-Whitney.

$$ \begin{equation} U_{1}=n_{1} n_{2}+\frac{n_{1}\left(n_{1}+1\right)}{2}-R_{1} \end{equation} $$ $$ \begin{equation} U_{2}=n_{1} n_{2}+\frac{n_{2}\left(n_{2}+1\right)}{2}-R_{2} \end{equation} $$

• \(n_{1}=\) tamaño de la muestra del grupo 1.
• \(n_{2}=\) tamaño de la muestra del grupo 2.
• \(R_{1}=\) sumatorio de los rangos del grupo 1.
• \(R_{2}=\) sumatorio de los rangos del grupo 2.

R1 <- sum(1,5,6,2,10.5,3)
R2 <- sum(10.5,12,4,8,9,7)
n1 <- length(muestraX)
n2 <- length(muestraY)
U1 <- (n1 * n2) + (n1*(n1 + 1) / 2) - R1
U2 <- (n1 * n2) + (n2*(n2 + 1) / 2) - R2
U  <- min(c(U1,U2))
U

[1] 6.5

Cálculo de p-value

Una vez ha obtenido el valor del estadístico U se puede calcular cual es la probabilidad de que adquiera un valor igual o más extremo que el observado. Si el tamaño de las muestras es inferior a 10, se compara el valor obtenido de U con los valores de una tabla U de Mann-Whitney. Si el U es menor que el valor correspondiente en la tabla, la diferencia es significativa. En este caso, el valor de la tabla para α=0.05, n1=6 y n2=6 es de 5. Dado que U obtenido es >5 no se considera significativa la diferencia. Si n1>10 y n2>10 se puede asumir que U se distribuye de forma aproximadamente normal, rechazando H0 si Z calculado es mayor que el valor de Z para el α elegido (este es método utilizado por defecto en R).

$$ \begin{equation} Z=\frac{U-\frac{n_{1} n_{2}}{2}}{\sqrt{\frac{n_{1} n_{2}\left(n_{1}+n_{2}+1\right)}{12}}} \sim N(0,1) \end{equation} $$

Cálculo del tamaño del efecto (side effect)

Como en todo test estadístico, no solo hay que indicar el p-value sino también el tamaño del efecto observado, ya que esto permitirá saber si, además de significativa, la diferencia es práctica. El tamaño del efecto para un test de Mann–Whitney–Wilcoxon se calcula a partir del Z-factor (es necesario haber asumido que U se distribuye ~ Normal).

$$ \begin{equation} r=\left|\frac{Z}{\sqrt{N}}\right| \end{equation} $$

N es el número total de observaciones, n1 + n2.

Una de las clasificaciones del tamaño más utilizada es:

• \(0.1 =\) pequeño
• \(0.3 =\) mediano
• \(≥0.5=\) grande

Ejemplo: Solución con R

R contiene una función llamada wilcox.test() que realiza un test de Mann–Whitney–Wilcoxon entre dos muestras cuando se indica que paired = False y además genera el intervalo de confianza para la diferencia de localización.

wilcox.test(x = muestraX, y = muestraY, alternative = "two.sided", mu = 0,
            paired = FALSE, conf.int = 0.95)

	Wilcoxon rank sum test with continuity correction

data:  muestraX and muestraY
W = 6.5, p-value = 0.07765
alternative hypothesis: true location shift is not equal to 0
95 percent confidence interval:
 -4.9000274  0.4000139
sample estimates:
difference in location 
             -2.390035 

En la salida devuelta por la función, el valor W equivale a U.

Cuando hay ligaduras o ties, la función wilcox.test() no es capaz de calcular el \(p-value\) exacto por lo que devuelve una aproximación asumiendo que \(U\) se distribuye de forma ~ normal. En estos casos, o cuando los tamaños muestrales son mayores de 20 y se quiere la aproximación por la normal, es más recomendable emplear la función wilcox_test() del paquete coin.

library(coin)
# La función wilcox.test() del paquete coin requiere pasarle los argumentos en
# forma de función (~), por lo que los datos tienen que estar almacenados en
# forma de data frame.
datos <- data.frame(
          grupo   = as.factor(rep(c("A", "B"), c(6, 6))),
          valores = c(muestraX, muestraY))

wilcox_test(valores ~ grupo, data = datos, distribution = "exact", conf.int=0.95)

	Exact Wilcoxon-Mann-Whitney Test

data:  valores by grupo (A, B)
Z = -1.8447, p-value = 0.06926
alternative hypothesis: true mu is not equal to 0
95 percent confidence interval:
 -4.9  0.4
sample estimates:
difference in location 
                  -2.4 

Resultado

La diferencia entre las probabilidades de que observaciones de una población superen a las de la otra no difiere de forma significativa (p-value = 0.06926). El tamaño del efecto observado es grande (0.53) pero no significativo.

Comparación entre t-test y test de Mann–Whitney–Wilcoxon

Una de las aplicaciones más frecuentes del test de Mann–Whitney–Wilcoxon es su uso como alternativa al t-test cuando las muestras no proceden de poblaciones con distribución normal (asimetría o colas) o porque tienen un tamaño demasiado reducido para poder afirmarlo. Es importante tener en cuenta que, aunque ambos test permiten realizar inferencia sobre la diferencia entre poblaciones, las hipótesis contrastadas no son las mismas. Mientras que el t-test siempre compara las medias de los grupos, el test de Mann–Whitney–Wilcoxon es menos específico. Si las distribuciones de las poblaciones subyacentes se diferencian únicamente en localización, entonces el test de Mann–Whitney–Wilcoxon compara medianas, para el resto de escenarios (poblaciones con distinta distribución, dispersión, asimetría…) contrasta si P(X>Y)=P(Y>X).

En este segundo caso la interpretación de los p-values no es tan directa. Es debido a esta naturaleza flexible por lo que hay que ser cauteloso con el test de Mann–Whitney–Wilcoxon. Por ejemplo, si las dos muestras comparadas proceden de poblaciones con asimetrías en direcciones opuestas, a pesar de que tanto la media como la mediana sean exactamente las mismas en ambos grupos, el p-value obtenido puede ser muy bajo.

En la práctica, el escenario en el que la única diferencia entre poblaciones es la localización es poco realista. Si las distribuciones tienen colas (asimetría) y las medias o medianas son distintas, es muy probable que las varianzas también lo sean. De hecho, la distribución normal es la única distribución estándar en la que la media y la varianza son independientes. Por lo tanto, si el test de Mann–Whitney–Wilcoxon se está aplicando por falta de normalidad y las medias-medianas no son iguales, lo más seguro es que no se cumpla con total rigurosidad la igualdad de varianzas. Es necesario evaluar estas características para poder determinar si el test de Mann–Whitney–Wilcoxon es suficientemente robusto para el estudio en cuestión.

Cuando la hipótesis que se quiere contrastar tiene que ser exclusivamente la igualdad de medianas se puede recurrir a la regresión de cuantiles, en concreto al cuantil 0.5.

Test de Mann–Whitney–Wilcoxon aplicado a muestras con asimetría opuesta

Supóngase que se dispone de las siguientes muestras y de que se desea conocer si existe diferencia significativa entre las poblaciones de origen.

grupo_a <- c(5, 5, 5, 5, 5, 5, 7, 8, 9, 10)
grupo_b <- c(1, 2, 3 ,4, 5, 5, 5, 5, 5, 5)
par(mfrow = c(1,2))
hist(grupo_a, col = "cyan4", main = "")
hist(grupo_b, col = "firebrick", main = "")

Output

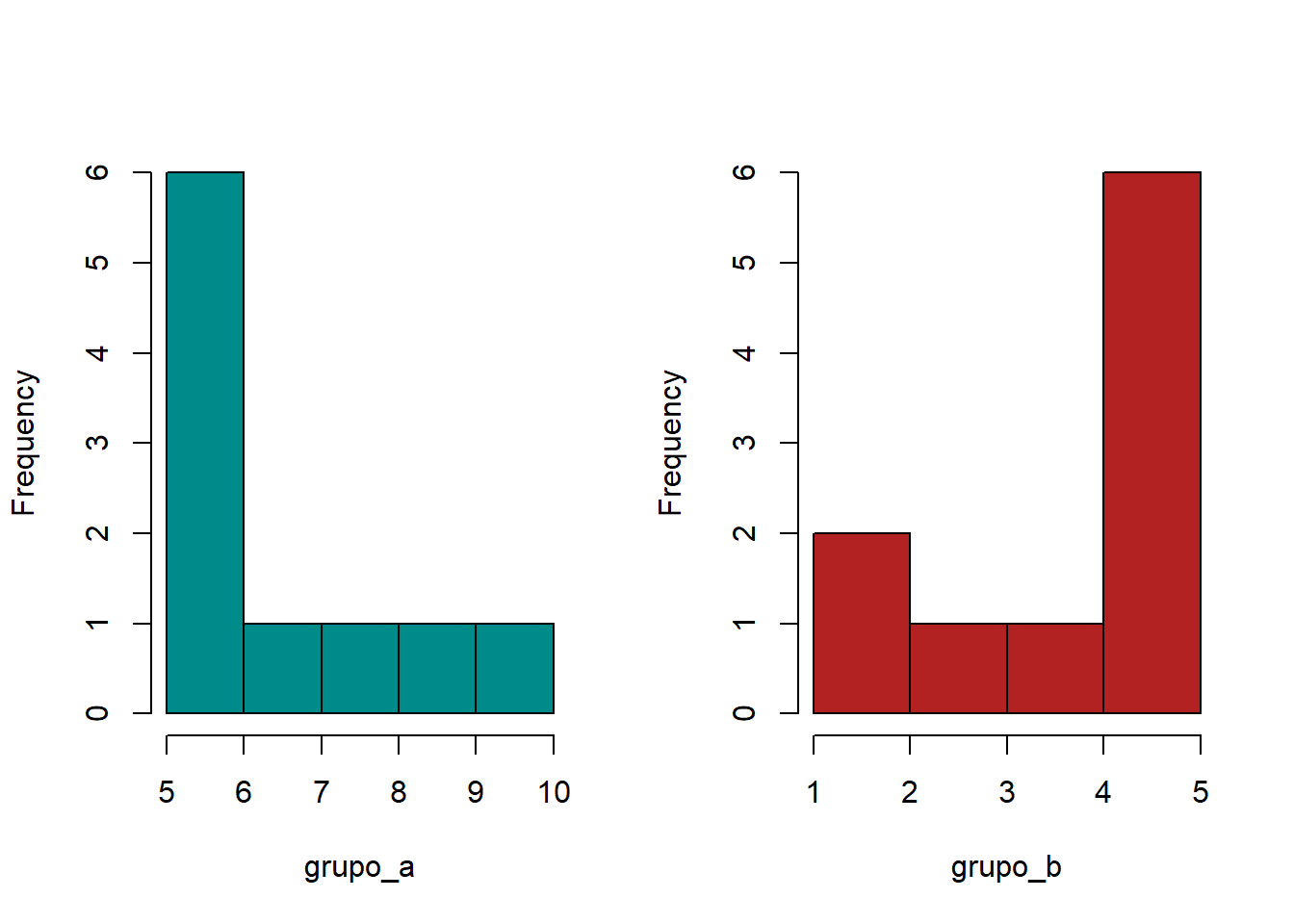
En vista de que el tamaño muestral es pequeño y de que ambos grupos muestran una clara asimetría, el t-test queda descartado. Una posible alternativa es emplear el test de Mann–Whitney–Wilcoxon con la intención de comparar las medianas.

wilcox.test(grupo_a, grupo_b, paired = FALSE)

	Wilcoxon rank sum test with continuity correction

data:  grupo_a and grupo_b
W = 82, p-value = 0.007196
alternative hypothesis: true location shift is not equal to 0

El p-value obtenido indica claras evidencias en contra de la hipótesis nula de que las medianas de ambos grupos son iguales. Sin embargo, si se calculan las medianas de las muestras, el resultado es el mismo.

median(grupo_a)

[1] 5

median(grupo_b)

[1] 5

¿Cómo es posible que, siendo las medianas exactamente las mismas, el p-value obtenido en el test sea significativo? En este caso, el problema no se encuentra en el test de Mann–Whitney–Wilcoxon en sí mismo, sino en la aplicación que se le quiere dar. Como las dos poblaciones tienen asimetrías en direcciones opuestas, es decir, sus diferencias van más allá de la localización, el test de Mann–Whitney–Wilcoxon no puede emplearse para comparar medianas. Lo que nos está indicando es que existen evidencias suficientes para afirmar que los miembros de un grupo tienen mayor probabilidad a estar por encima de los del otro.

Potencial problema del test de Mann–Whitney–Wilcoxon con tamaños muestrales grandes

Suele recomendarse emplear el test de Mann–Whitney–Wilcoxon en lugar del t-test cuando los tamaños muestrales son pequeños y no se tiene evidencias de que las poblaciones de origen siguen una distribución normal. Si bien esta práctica está bastante fundamentada, no hay que confundirla con la de utilizar el test de Mann–Whitney–Wilcoxon como alternativa al t-test siempre que no se cumpla la normalidad y sin tener en cuenta el tamaño muestral. A medida que el número de observaciones aumenta, también lo hace la robustez del t-test frente a desviaciones de la normalidad. Por otro lado, el test de Mann–Whitney–Wilcoxon incrementa su sensibilidad a diferencias más allá de las medianas. Por ejemplo, aumenta el poder estadístico de detectar diferencias significativas en la probabilidad de que observaciones de un grupo superen a las del otro debido únicamente a diferencias en la dispersión de las poblaciones de origen y no porque sus medianas sean distintas. Si el objetivo del estudio es identificar cualquier diferencia distribucional, esto no supone un problema, pero si lo que se quiere comparar son las medianas, se obtendrán p-values que no se corresponden con la pregunta que el investigador quiere responder.

Considérese dos muestras que proceden de dos poblaciones distintas, una con distribución normal y otra con distribución log-normal (asimetría derecha). Ambas poblaciones tienen la misma mediana pero claramente siguen distribuciones distintas.

$$ \begin{equation} \text { Distribución normal : media }=\text { mediana } \end{equation} $$ $$ \begin{equation} \text { Distribución normal : media }=\exp \left(\mu+\frac{\sigma^{2}}{2}\right), \text { mediana }=\exp (\mu) \end{equation} $$

x <- seq(0, 5, length = 1000)
y <- dlnorm(x = x, meanlog =  0.5, sdlog = 1.7)
plot(x, y, type = "l", lty = 1, xlab = "x", col = "blue", ylab = "Densidad",
     main = "Distribuciones lognormal y normal con misma mediana", xlim=c(-5, 5))
x_2 <- seq(-5, 5, length = 1000)
y_2 <- dnorm(x = x_2, mean = 1.648721, sd = 1)
lines(x_2, y_2, col = "red")
legend("topright",
       legend = c("mediana lognormal = 0.5", "mediana normal = 0.5"),
       col = c("blue", "red"), lty = 1,cex = 0.7)

Output

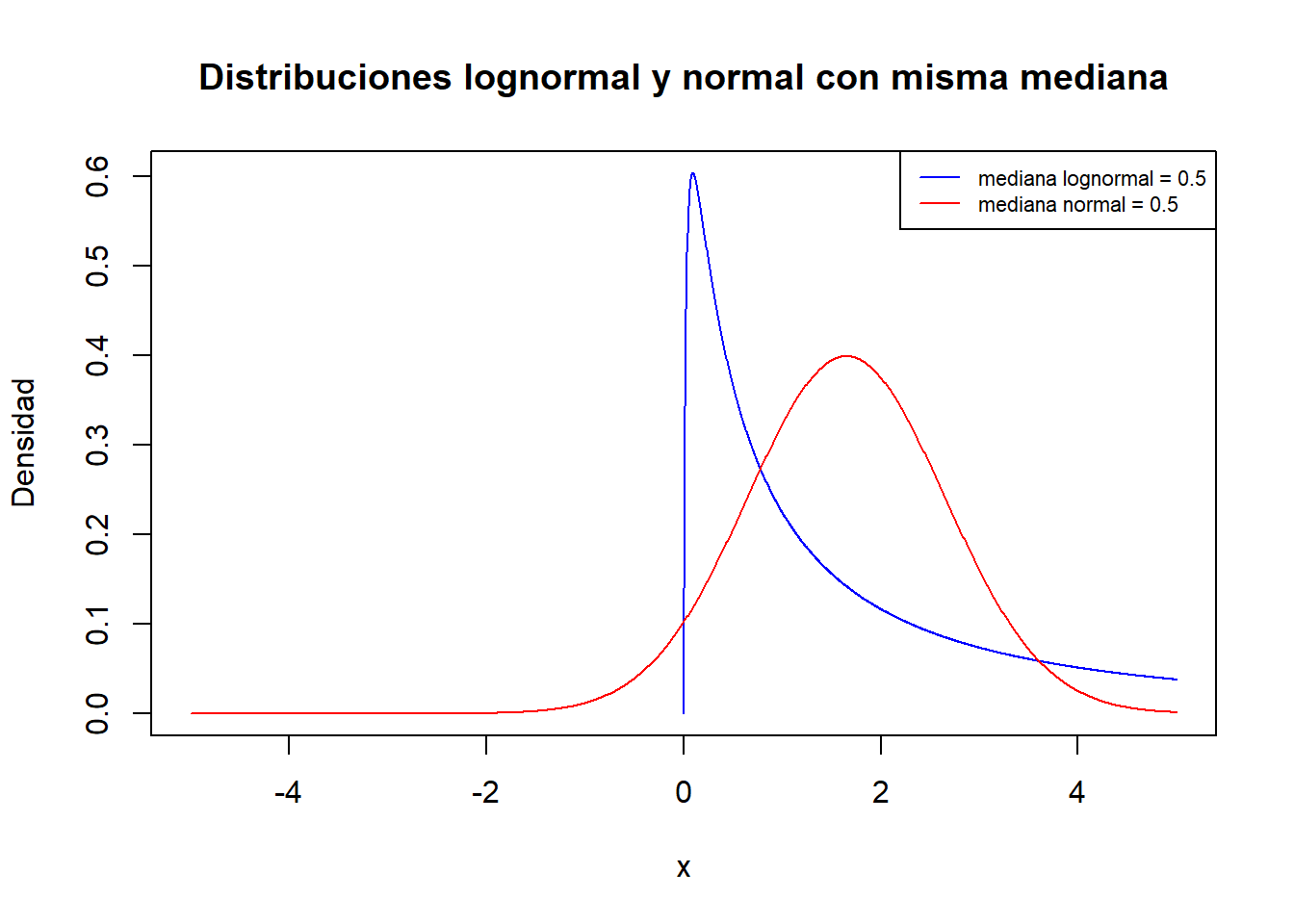
Supóngase ahora que el investigador, que desconoce la distribución real de las poblaciones, obtiene dos muestras de 20 observaciones cada una.

set.seed(888)
muestra_a <- rlnorm(n = 20, meanlog =  0.5, sdlog = 1.7)
muestra_b <- rnorm(n = 20, mean = 1.648721, sd = 1)
par(mfrow = c(1,2))
hist(muestra_a, breaks = 10, main = "", col = "blue")
hist(muestra_b, breaks = 10, main = "", col = "firebrick")

Output

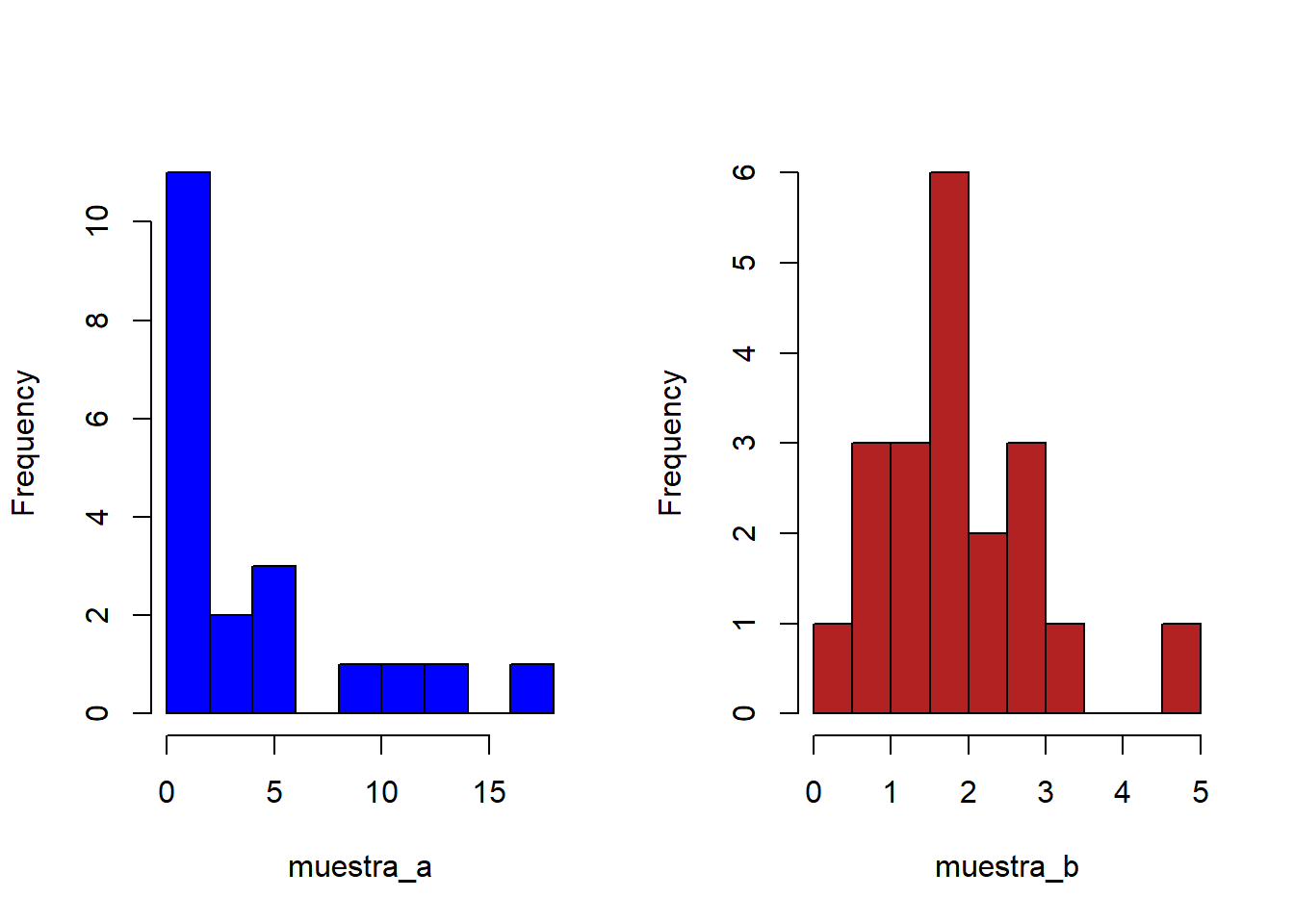
Con base en la falta de normalidad de la muestra a, el investigador considera que el t-test no es adecuado para comparar la localización de las poblaciones y decide que quiere comparar medianas con el test de Mann–Whitney–Wilcoxon.

wilcox.test(muestra_a, muestra_b, paired = FALSE)

	Wilcoxon rank sum exact test

data:  muestra_a and muestra_b
W = 196, p-value = 0.9254
alternative hypothesis: true location shift is not equal to 0

El resultado le indica que no hay evidencias para considerar que la localización de las poblaciones es distinta y concluye que las medianas de ambas poblaciones son iguales.

Véase lo que ocurre si el tamaño muestral se incrementa de 20 a 1000 observaciones.

set.seed(888)
muestra_a <- rlnorm(n = 1000, meanlog =  0.5, sdlog = 1.7)
muestra_b <- rnorm(n = 1000, mean = 1.648721, sd = 1)
wilcox.test(muestra_a,muestra_b, paired = FALSE)

	Wilcoxon rank sum test with continuity correction

data:  muestra_a and muestra_b
W = 551900, p-value = 5.842e-05
alternative hypothesis: true location shift is not equal to 0

En este caso, la conclusión obtenida es totalmente opuesta, hay muchas evidencias en contra de la hipótesis nula de que ambas poblaciones tienen la misma localización por lo que el investigador podría concluir erróneamente que las medianas de ambas poblaciones son distintas.

Este ejemplo pone de manifiesto la importancia que tiene el tamaño muestral en la potencia del test de Mann–Whitney–Wilcoxon y la necesidad de entender que, si las distribuciones no son iguales a excepción de su localización, el test es muy sensible detectando diferencias en las distribuciones a pesar de que sus medianas sean las mismas. En este caso, el investigador solo podría concluir que hay evidencias de que la distribución de las dos poblaciones se diferencia en algún aspecto, pero no podría concretar cuál.

Conclusión

El test de Mann–Whitney–Wilcoxon (WMW) es un test no paramétrico que contrasta si dos muestras proceden de poblaciones equidistribuidas.

Referencias

• OpenIntro Statistics: Fourth Edition by David Diez, Mine Çetinkaya-Rundel, Christopher Barr libro
• Handbook of Biological Statistics by John H. McDonald