
Inferencia de variables categóricas en R
Índice de contenido
Resumen:
Inferencia de variables categóricas o proporciones. Intervalos de confianza y test de hipótesis.
¿Cómo citar el presente artículo?
Romero, J. (Enero 1, 2019). Inferencia de variables categóricas en R. R.JeshuaRomeroGuadarrama. https://www.r.jeshuaromeroguadarrama.com/es/blog/applied-statistics/categorical-variable-inference/.
Inferencia de variables categóricas en R by Jeshua Romero Guadarrama, available under Attribution 4.0 International (CC BY 4.0) at https://www.r.jeshuaromeroguadarrama.com/es/blog/applied-statistics/categorical-variable-inference/.
Introducción
Cuando se trabaja con variables dicotómicas o de Bernoulli, variables cuyo resultado es verdadero con una probabilidad \(p\), se pueden presentar diferentes estudios:
- Conocer el intervalo dentro del cual se encuentra la proporción de casos verdaderos ($p$) de una población.
- Realizar un test de hipótesis para determinar si la proporción observada se corresponde con la esperada.
- Conocer el intervalo de confianza para la diferencia en las proporciones de eventos verdaderos entre dos poblaciones.
- Realizar un test de hipótesis para determinar si la diferencia en las proporciones de dos poblaciones es significativa.
Estas situaciones se pueden resolver aplicando el teorema del límite central a la distribución binomial, que es la distribución que explica el comportamiento de una sucesión de variables de Bernoulli:
$$
\begin{equation} X=X_{1}+\ldots+X_{n} B(n, p) \end{equation}
$$
Supóngase un conjunto de variables de Bernoulli (eventos) ($X_{1}, X_{2} \ldots X_{n}$) en el que el resultado de cada uno puede ser verdadero o falso.
Si se desea conocer la probabilidad \(p\) con la que ocurre el resultado verdadero, la forma de hacerlo es calcular la proporción de resultados verdaderos respecto del total de casos.
$$
\begin{equation} p=\frac{X_{\text {verdadero }}}{N} \end{equation}
$$
Dado que por lo general no se dispone de información de toda la población, se emplea como estimador insesgado de la proporción poblacional ($p$) la proporción muestral ($\hat{p}$)
$$
\begin{equation} \hat{p}=\frac{X_{\text {verdadero }}}{n} \end{equation}
$$
La distribución binomial tiene entre sus múltiples características que si el valor de \(n\) es suficientemente grande y el valor de \(p\) no está demasiado próximo a sus valores extremos \(0\) o \(1\), entonces su distribución se aproxima a una distribución normal centrada en la media de la distribución binomial y con desviación estándar equivalente a la desviación de la distribución binomial. Ver más adelante las condiciones para esta aproximación.
$$
\begin{equation} S i X=B(n, p) \text { entonces } X \sim N(n p, n q p) \end{equation}
$$
Dado que el estimador \(\hat{p}\) no es más que una transformación de \(X\) dividida por el número de observaciones:
$$
\begin{equation} \hat{p}=\frac{X}{n} \text { entonces } \hat{p} \sim N(p, \frac{p q}{n}) \end{equation}
$$
Una vez aproximada la distribución binomial a una distribución normal, se puede tipificar el valor estimado \(\hat{p}\) y utilizar los \(z-score\) para hacer inferencia.
$$
\begin{equation} Z_{\text {calculado }}=\frac{\hat{p}-p_{0}}{\sqrt{\frac{\hat{q} \hat{p}}{n}}} \end{equation}
$$
siendo \(p_{0}\) el valor considerado en la hipótesis nula como el verdadero valor de \(p\) en la población.
Condiciones para aplicar el TLC a una distribución binomial
Las condiciones para poder aplicar el teorema del límite central a una distribución binomial son:
Independencia: Las observaciones deben de ser independientes unas de otras. Para ello, las observaciones de la muestra tienen que haber sido seleccionadas al azar y el tamaño muestral tiene que ser menor al
\(10\%\)de la población.Tamaño mínimo de la muestra:
- Para intervalos de confianza: La muestra debe de contener al menos
\(10\)observaciones verdaderas y\(10\)observaciones falsas. - Para test de hipótesis: El tamaño de la muestra debe ser tal que, el número de eventos verdaderos y el número de eventos falsos esperados acorde a la hipótesis nula sea mayor de
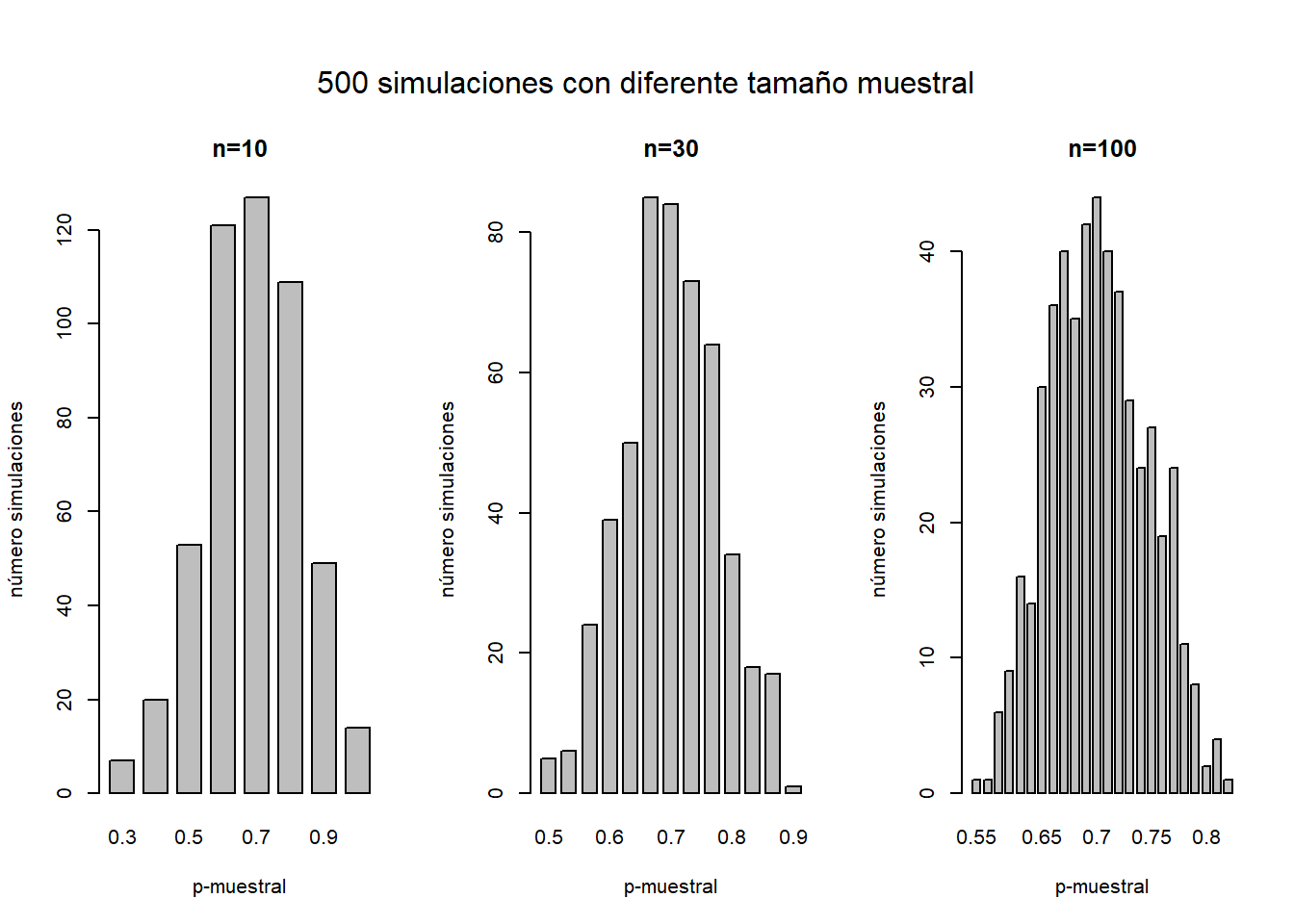
\(10\)en ambos casos.\(n p_{0}>10 \& n(1-p_{0})>10\) - A esto se le conoce como “success-failure condition”. Si no se cumple esta condición la aproximación a la distribución normal no es buena y por lo tanto tampoco los resultados de la inferencia. En los siguientes gráficos se muestra el resultado de simular
\(500\)muestras de tamaños\(10\),\(30\)y\(100\)observaciones todas ellas con una proporción de eventos verdaderos\(p = 0.7\). Se observa que a medida que aumenta el tamaño muestral, la distribución se aproxima más a una normal centrada en el valor\(p\).
- Para intervalos de confianza: La muestra debe de contener al menos
set.seed(12345)
par(mfrow = c(1, 3))
# Genera 4 líneas de espacio en el margen superior de la imagen
par(oma = c(0, 0, 4, 0))
barplot(table(rbinom(500, 10, 0.7)/10), space = 0.4, main = "n=10",
ylab = "número simulaciones", xlab = "p-muestral")
barplot(table(rbinom(500, 30, 0.7)/30), space = 0.4, main = "n=30",
ylab = "número simulaciones", xlab = "p-muestral")
barplot(table(rbinom(500, 100, 0.7)/100), space = 0.4, main = "n=100",
ylab = "número simulaciones", xlab = "p-muestral")
mtext(text = "500 simulaciones con diferente tamaño muestral",
outer = TRUE, cex = 1)
par(mfrow = c(1, 1))
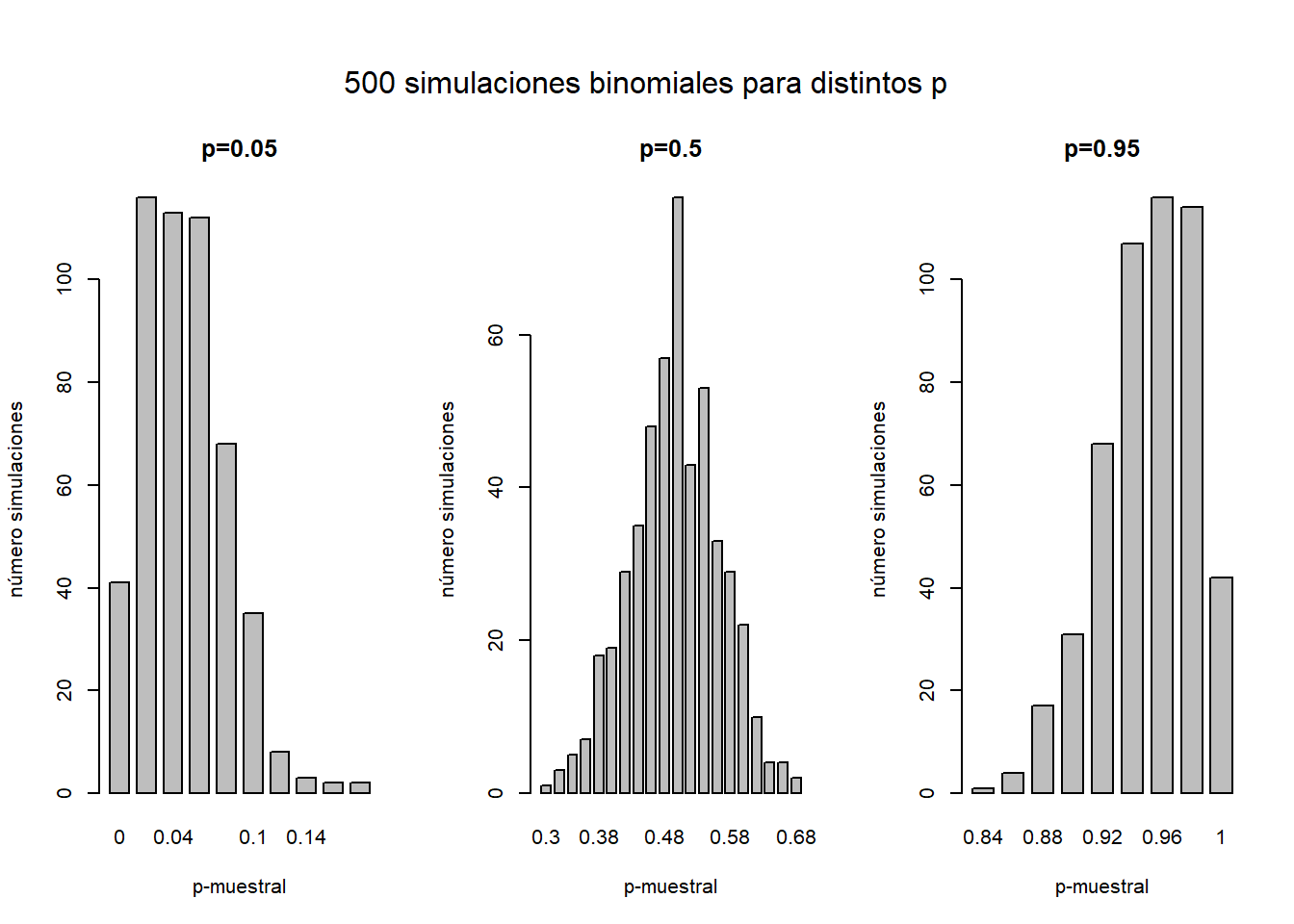
La razón por la que la aproximación de una binomial a una normal solo se puede considerar valida cuando el valor \(p\) es próximo a \(0.5\) se debe a que una distribución normal es simétrica con colas asintóticas.
Sin embargo, los valores de una proporción están acotados entre \(0\) y \(1\). Si el valor \(p\) se aproxima mucho a uno de los extremos, la distribución obtenida va a ser asimétrica, puesto que se cortará en uno de los extremos.
Véase en las siguientes simulaciones como se vuelve asimétrica la distribución cuando los valores de \(p\) se aproximan a \(0\) o a \(1\).
par(mfrow = c(1, 3))
# Genera 4 líneas de espacio en el margen superior de la imagen
par(oma = c(0, 0, 4, 0))
barplot(table(rbinom(500, 50, 0.05)/50), space = 0.4, main = "p=0.05",
ylab = "número simulaciones", xlab = "p-muestral")
barplot(table(rbinom(500, 50, 0.5)/50), space = 0.4, main = "p=0.5",
ylab = "número simulaciones", xlab = "p-muestral")
barplot(table(rbinom(500, 50, 0.95)/50), space = 0.4, main = "p=0.95",
ylab = "número simulaciones", xlab = "p-muestral")
mtext(text = "500 simulaciones binomiales para distintos p", outer = TRUE,
cex = 1)
par(mfrow = c(1, 1))
Intervalo de confianza para una proporción
Cuando el objetivo del estudio es conocer el verdadero valor de una proporción en una población a partir de una muestra obtenida de dicha población, se recurre a los intervalos de confianza.
El parámetro de interés es la proporción de eventos verdaderos en la población ($p$), el estadístico empleado como estimador insesngado es la proporción en la muestra ($\hat{p}$).
La estructura de todo intervalo de confianza es:
$$ \text { estadistico } \pm \text { margen de error } $$
En el caso de proporciones, habiendo considerado válida la aproximación de la distribución binomial a una normal, el intervalo de confianza con seguridad de \(1−\alpha\) se corresponde con:
$$
\begin{equation} [\hat{p} \pm Z_{1-\alpha / 2} * \sqrt{\frac{\hat{p} \hat{q}}{n}}] \end{equation}
$$
siendo \(Z_{1-\alpha / 2}\) el cuantil en valor absoluto de una distribución normal tipificada \(N(0, 1)\) tal que el un porcentaje de densidad igual a \(1 − \alpha\) queda comprendido entre \(-Z\) y \(+Z\).
Ejemplo
Se pretende estimar el resultado de un referéndum a partir de una muestra de la población. La encuesta realizada sobre un total de \(100\) personas seleccionadas de forma aleatoria ha resultado en \(35\) personas a favor de la propuesta y \(65\) en contra (se considera que no existen indecisos para poder tratar a la variable como dicotómica) ¿Cuál es el intervalo de confianza del \(95\%\) para el resultado de la votación?
Se trata de un conjunto de eventos cuyo resultado puede ser considerado como verdadero o falso. Son por lo tanto variables de Bernoulli cuyo conjunto sigue una distribución binomial. Sí se cumplen las condiciones, esta distribución puede ser aproximada a una Normal permitiendo realizar inferencia basada en el TLC.
Condiciones para la aproximación de una binomial a una normal:
- Independencia: Los individuos se ha seleccionado de forma aleatoria y el tamaño de la muestra ($n = 100$) es menor que el
\(10\%\)de la población. - Tamaño mínimo: Se ha de cumplir que la muestra contenga al menos
\(10\)eventos verdaderos y\(10\)eventos falsos:- Verdadero
\(= 35 > 10\) - Falso
\(= 65 > 10\)
- Verdadero
Se cumplen las condiciones para aplicar el TLC.
El valor muestral de la proporción (estadístico) ha resultado ser \(\hat{p}=\frac{35}{100}=0.35\)
El error estándar (SE) de una proporción:
$$
\begin{equation} S E=\sqrt{\frac{\hat{q} \hat{p}}{n}}=\sqrt{\frac{0.35 * 0.65}{100}}=0.04769696 \end{equation}
$$
\(Z-value\) para el nivel de significancia \(\alpha\) del intervalo:
$$
\begin{equation} \alpha=0.05 \end{equation}
$$
$$
\begin{equation} Z_{1-\alpha / 2}=\text { qnorm }(p=1-0.05 / 2, \text { mean }=0, s d=1, \text { lower.tail }=T R U E)=1.96 \end{equation}
$$
Intervalo de confianza:
$$
\begin{equation} p=[0.35 \pm 1.96 * 0.04769696]=[0.35 \pm 0.09348604]=[0.257,0.443] \end{equation}
$$
Con la muestra disponible se tiene un error de \(9.3\) puntos para un nivel de confianza del \(95\%\).
Solución con R
La función prop.test() que permite hacer test de hipótesis con proporciones para una o dos poblaciones. Además devuelve el intervalo de confianza para el verdadero valor de la proporción o para la diferencia de proporciones. Implementa la posibilidad de incluir la corrección de continuidad de Yates si el tamaño muestral es pequeño.
prop.test(x = 35, n = 100, conf.level = 0.95, correct = FALSE)
1-sample proportions test without continuity correction
data: 35 out of 100, null probability 0.5
X-squared = 9, df = 1, p-value = 0.0027
alternative hypothesis: true p is not equal to 0.5
95 percent confidence interval:
0.2636425 0.4474556
sample estimates:
p
0.35
prop.test(x = 35, n = 100, conf.level = 0.95, correct = TRUE)
1-sample proportions test with continuity correction
data: 35 out of 100, null probability 0.5
X-squared = 8.41, df = 1, p-value = 0.003732
alternative hypothesis: true p is not equal to 0.5
95 percent confidence interval:
0.2591235 0.4525560
sample estimates:
p
0.35
Test de hipótesis para una proporción
Tal y como se ha visto en la introducción, si se cumplen las condiciones para aproximar una distribución binomial a una normal, ocurre que:
$$
\begin{equation} \hat{p} \sim N(p, n q p) \end{equation}
$$
Esto permite trabajar con los \(Z-score\) de una normal tipificada y por lo tanto obtener la probabilidad de que ocurran valores igual o más extremos que los observados.
$$
\begin{equation} Z_{\text {calculado }}=\frac{\hat{p}-p_{0}}{\sqrt{\frac{q_{0} p_{0}}{n}}} \end{equation}
$$
siendo \(p_{0}\) el valor considerado en la hipótesis nula como el verdadero valor de \(p\) en la población.
Si \(|Z_{\text {calculado }}|>Z_{1-\alpha / 2}\) se rechaza la hipótesis nula en favor de la alternativa.
Ejemplo I
Una encuesta realizada en México concluye que el \(60\%\) de los \(1983\) mexicanos entrevistados, elegidos de forma aleatoria, aceptaban la teoría de la evolución. ¿Se puede afirmar, en base a los resultados, que la mayoría de mexicanos aceptan la evolución con un nivel de significancia del \(5\%\)?
1. Hipótesis
\(H_{0}\): No hay ni mayoría ni minoría ($50%$ de cada tendencia), \(p_{0} = 0.5\).
\(H_{a}\): Existe una mayoría que acepta la evolución, es decir, más de la mitad lo hace. \(p_{0} > 0.5\).
2. Estadístico
Se emplea como estimador insesgado de la proporción poblacional ($p$) la proporción observada en la muestra ($\hat{p}$).
3. Condiciones para la aproximación de una binomial a una normal
- Independencia: Los individuos se han seleccionado de forma aleatoria y el tamaño de la muestra es menor que el 10% de la población.
- Tamaño mínimo: Se ha de cumplir que la muestra contenga al menos
\(10\)eventos verdaderos y\(10\)eventos falsos acorde con la hipótesis nula:- Verdadero
\(= 0.5*1983 = 991.5\). - Falso
\(= 0.5*1983 = 991.5\).
- Verdadero
El valor \(p\) considerado en la hipótesis nula no es próximo a \(0\) ni a \(1\). Se cumplen las condiciones para aplicar el TCL.
4. Límite de significancia
$$
\begin{equation} \alpha=0.05 \end{equation}
$$
5. Cálculo de p-value
Calculo del valor \(Z\) observado
$$
\begin{equation} Z_{\text {calculado }}=\frac{0.6-0.5}{\sqrt{\frac{0.5 * 0.5}{1983}}}=8.92 \end{equation}
$$
$$
\begin{equation} p-value = P(p>0.6)=P(Z>8.92)= \end{equation}
$$
$$
\begin{equation} 1-\text { pnorm }(q=8.92, \text { mean }=0, s d=1, \text { lower. tail }=T R U E) \simeq 0 \end{equation}
$$
6. Conclusión
Dado que el \(p-value\) obtenido es menor que el valor de significancia alpha, se rechaza la hipótesis nula en favor de la hipótesis alternativa.
Sí hay evidencias significativas para considerar que la mayoría de la población acepta la evolución.
Solución con R
prop.test(x = 0.6*1983, n = 1983, p = 0.5, alternative = "greater",
conf.level = 0.95, correct = FALSE)
1-sample proportions test without continuity correction
data: 0.6 * 1983 out of 1983, null probability 0.5
X-squared = 79.32, df = 1, p-value < 2.2e-16
alternative hypothesis: true p is greater than 0.5
95 percent confidence interval:
0.58178 1.00000
sample estimates:
p
0.6
Ejemplo II
Se cree que una determinada enfermedad tiene más prevalencia en hombres que en mujeres. Para determinar si es cierto se elige una muestra aleatoria de \(100\) enfermos y se observa que de ellos \(70\) son hombres. ¿Qué se puede concluir con un nivel de significancia del \(5\%\)?
Considérese \(p\) como la proporción de hombres que existen en la población de enfermos. Se quieren encontrar evidencias a favor de la hipótesis de que \(p > 0.5\) (hipótesis alternativa), partiendo de la hipótesis nula de que la enfermedad se reparte de forma igual entre ambos sexos.
$$
\begin{equation} H_{0}: p=0.5 \end{equation}
$$
Dado que se cumplen las condiciones para aproximar la distribución binomial a una normal, se puede realizar un contraste de hipótesis para una proporción.
prop.test(x = 70, n = 100, p = 0.5, alternative = "greater", conf.level = 0.95,
correct = FALSE)
1-sample proportions test without continuity correction
data: 70 out of 100, null probability 0.5
X-squared = 16, df = 1, p-value = 3.167e-05
alternative hypothesis: true p is greater than 0.5
95 percent confidence interval:
0.6201679 1.0000000
sample estimates:
p
0.7
Potencia de contraste y tamaño de las muestras
Siendo la estructura de un intervalo de confianza \([.\) estadistico \(.\pm Z_{1-\alpha / 2} * S E]\), la amplitud del intervalo viene dada por el margen de error \(Z_{1-\alpha / 2} * S E\).
Si se desea reducir el intervalo para ser más preciso en la acotación del valor sobre el que se esta haciendo inferencia (en este caso p) se puede:
Reducir el porcentaje de confianza del intervalo, lo que generaría valores de
\(Z\)menores. Sin embargo, esto significaría perder precisión en la estimación, puesto que se incrementa la probabilidad de dejar fuera del intervalo al verdadero valor del parámetro poblacional.Incrementar el tamaño de la muestra y con ello reducir el
\(SE\). En el caso de proporciones se cumple que para un determinado margen de error:
$$
\begin{equation} \text { margen de error }=Z_{1-\alpha / 2} * \sqrt{\frac{\hat{q} \hat{p}}{n}} ; n \geq \hat{p} \hat{q} \frac{Z_{1-\alpha / 2}^{2}}{\text { margen de error }{ }^{2}} \end{equation}
$$
En el diseño experimental es crítico calcular de antemano el tamaño de la muestra que se requiere para alcanzar la precisión deseada. De lo contrario se pueden estar invirtiendo más recursos de los realmente necesarios o bien darse cuenta a posteriori de que el experimento no es concluyente por no haber realizado un muestreo lo suficientemente grande.
El cálculo del tamaño de la muestra \(n \geq \hat{p} \hat{q} \frac{Z_{1-\alpha / 2}^{2}}{\text { margen de error }{ }^{2}}\) requiere conocer el valor de \(p\) y \(q\) o de sus estimadores muestrales.
Sin embargo, dado que este es cálculo hace antes de realizar el experimento, difícilmente se van a conocer. Existen varias opciones para encontrar valores útiles:
- Recurrir estudios previos en los que se pueda haber obtenido el valor de
\(p\)en la población. - Obtener una muestra piloto: Una pequeña muestra inicial a partir de la cual estimar
\(\hat{p}\). - Si no se dispone de ninguna información se recurre al supuesto más escéptico, que la proporción de eventos verdaderos es del
\(50\%\),\(p = 0.5\).
El paquete pwr contiene una extensión de los test de potencia más empleados para distintos contrastes. Entre sus características está la de ser capaz de calcular la potencia cuando los grupos tienen diferente número de observaciones. También es capaz de devolver el tamaño que deben tener las muestras para alcanzar un determinado tamaño de efecto (effect size).
| Función | Cálculo de potencia para: |
|---|---|
| pwr.2p.test | dos proporciones ($n$ igual) |
| pwr.2p2n.test | dos proporciones ($n$ desigual) |
| pwr.anova.test | ANOVA unidireccional equilibrada |
| pwr.chisq.test | prueba de chi-cuadrado |
| pwr.f2.test | modelo linear general |
| pwr.p.test | proporción (una muestra) |
| pwr.r.test | correlación |
| pwr.t.test | t-tests (una muestra, dos muestras, emparejados o pareados) |
| pwr.t2n.test | t-test (dos muestras con \(n\) desigual) |
Ejemplo I
Un equipo de investigación quiere hacer una estimación del resultado de una votación en la que las posibilidades son \(Sí/No\). En el diseño epxerimental quieren determinar el número de personas a las que se tiene que consultar para lograr crear un intervalo de confianza del \(97\%\) de seguridad con un margen de error de 1 punto ($0.01%$).
$$
\begin{equation} n \geq \hat{p} \hat{q} \frac{Z_{1-\alpha / 2}^{2}}{\text { margen de error }} \end{equation}
$$
Dado que se desconoce cuál es la proporción de votantes que están a favor (Si), se debe tomar como estimación la situación más neutral \(p = 0.5\).
Nivel de significancia:
$$
\begin{equation} \alpha=1-0.97=0.03 \end{equation}
$$
El valor de \(Z_{1-\alpha / 2}\):
$$
\begin{equation} \text { : qnorm }(p=0.985, \text { mean }=0, s d=1, \text { lower.tail }=\text { TRUE })=2.17009 \end{equation}
$$
$$
\begin{equation} n \geq 0.5 * 0.5 \frac{2.17^{2}}{0.01^{2}}=11772.25 \end{equation}
$$
El tamaño mínimo debe ser de \(11773\) personas
Intervalo de confianza para la diferencia de proporciones en dos poblaciones independientes.
Considérense dos poblaciones de modo que en cada una de ellas se estudia la misma variable cualitativa dicotómica (Bernoulli), cada una de las poblaciones con una proporción de eventos verdaderos para esta variable ($p_{1}$ y \(p_{2}\)).
Si se dispone de una muestra de cada población ($n_{1}$ y \(n_{2}\)) y se cumplen para cada una de ellas las condiciones que permiten aproximar una distribución binomial a una distribución normal (explicadas en la introducción), se puede obtener un intervalo de confianza para la diferencia de las proporciones \(p\) entre ambas poblaciones tal que:
$$
\begin{equation} \text { estadistico } \pm Z_{1-\alpha / 2} * S E(\hat{p_{1}}-\hat{p_{2}}) \end{equation}
$$
$$
\begin{equation} (\hat{p}_{1}-\hat{p}_{2}) \pm Z_{1-\alpha / 2} * \sqrt{\frac{\hat{p}_{1} \hat{q}_{1}}{n_{1}}+\frac{\hat{p}_{2} \hat{q}_{2}}{n_{2}}} \end{equation}
$$
Ejemplo I
Una encuesta sobre el derecho a portar armas realizada en USA y en UE mostró los siguientes resultados. De los 1028 americanos encuestados \(257\) estaban en contra y de los \(83\) europeos entrevistados \(59\) lo estaban. En ambos casos se seleccionaron individuos aleatoriamente. ¿Cuál es la diferencia entre la proporción de americanos y europeos que rechazan la tenencia de armas? Utilizar un intervalo del \(95\%\).
| País | En contra | Total encuestados | $\hat{p}$ |
|---|---|---|---|
| USA | 257 | 1028 | $\frac{257}{1028} = 0.25$ |
| UE | 59 | 83 | $\frac{59}{83} = 0.71$ |
1. Condiciones para el TCL
Independencia:
- Dentro de cada muestra: Muestreo aleatorio,
\(n_{1} < 10\%\)\(población_{1}\)y\(n_{2} < 10\%\)\(población_{2}\). - Entre grupos/muestras: Los datos no son pareados.
Tamaño muestral:
- Muestra USA:
- Observaciones positivas
\(= 257 > 10\) - Observaciones negativas
\(= 771 > 10\)
- Observaciones positivas
- Muestra UE:
- Observaciones positivas
\(= 59 > 10\) - Observaciones negativas
\(= 24 > 10\)
- Observaciones positivas
Se cumplen las condiciones para aproximar ambas distribuciones binomiales a distribuciones normales.
2. Estadístico
$$
\begin{equation} (p_{E U}-p_{U S A})=0.71-0.25=0.46 \end{equation}
$$
3. Cálculo del SE para la diferencia de dos proporciones
$$
\begin{equation} S E=\sqrt{\frac{0.25(1-0.25)}{1028}+\frac{0.71(1-0.71)}{83}}=0.0516 \end{equation}
$$
4. Cálculo de Z para una confianza del 95%
$$
\begin{equation} Z_{1-\alpha / 2}=\text { qnorm }(p=0.975, \text { mean }=0, s d=1)=1.96 \end{equation}
$$
5. Intervalo
$$
\begin{equation} [0.46 \pm 1.96+0.516]=[0.36,0.56] \end{equation}
$$
Se puede afirmar con una seguridad del \(95\%\) que existe entre un \(36\%\) y un \(56\%\) más de oposición a la tenencia de armas en la población europea que en la americana.
Dado que el intervalo no incluye el valor \(0\), sabemos que la diferencia sí es significativa para un \(95\%\) de confianza.
Sin embargo para estudiar significancia es mejor calcular el \(p-value\) mediante un test de hipótesis.
Solución con R
prop.test(x = c(257, 59), n = c(1028, 83), conf.level = 0.95,
alternative = "two.sided", correct = FALSE)
2-sample test for equality of proportions without continuity
correction
data: c(257, 59) out of c(1028, 83)
X-squared = 80.138, df = 1, p-value < 2.2e-16
alternative hypothesis: two.sided
95 percent confidence interval:
-0.5619068 -0.3597799
sample estimates:
prop 1 prop 2
0.2500000 0.7108434
Ejemplo II
Se cree que la osteoporosis está relacionada con el sexo. Para estudiarlo se elige una muestra aleatoria de \(100\) hombres de más de \(50\) años y una muestra de \(200\) mujeres en las mismas condiciones.
Se observan \(10\) hombres y \(40\) mujeres con algún grado de osteoporosis. ¿Qué podemos concluir con una confianza del \(95\%\)?
Las condiciones para aplicar el TLC a proporciones se cumple, aunque en el caso de los hombres, el número de observaciones positivas está en el mínimo recomendado.
prop.test(x = c(10, 40), n = c(100, 200), alternative = "two.sided",
correct = FALSE)
2-sample test for equality of proportions without continuity
correction
data: c(10, 40) out of c(100, 200)
X-squared = 4.8, df = 1, p-value = 0.02846
alternative hypothesis: two.sided
95 percent confidence interval:
-0.18081139 -0.01918861
sample estimates:
prop 1 prop 2
0.1 0.2
Se tiene una confianza del \(95\%\) al afirmar que la osteoporosis incide entre un \(1.9\%\) y un \(18\%\) menos en hombres que en mujeres.
Test de hipótesis para la diferencia de proporciones en dos poblaciones independientes
Considérense dos poblaciones de modo que en cada una de ellas se estudia la misma variable cualitativa dicotómica (Bernoulli), cada una de las poblaciones con una proporción de eventos verdaderos para esta variable ($p_{1}$ y \(p_{2}\)).
Si se dispone de una muestra de cada población ($n_{1}$ y \(n_{2}\)) y se cumplen para cada una de ellas las condiciones que permiten aproximar una distribución binomial a una distribución normal (explicadas en la introducción), se puede estudiar la diferencia de proporciones entre dos poblaciones como si se estuviesen comparando dos distribuciones normales.
$$
\begin{equation} \hat{p}_{1} \sim N(p_{1}, \frac{p_{1} q_{1}}{n_{1}}) \end{equation}
$$
$$
\begin{equation} \hat{p}_{2} \sim N(p_{2}, \frac{p_{2} q_{2}}{n_{2}}) \end{equation}
$$
La diferencia de proporciones ($p_{1} − p_{2}$) se distribuye de forma normal y por lo tanto también la diferencia de los estimadores muestrales:
$$
\begin{equation} (\hat{p}_{1}-\hat{p}_{2}) \sim N(\underbrace{p_{1-p_{2}}}_{H_{0}}, S E=\sqrt{\frac{p_{1} q_{1}}{n_{1}}+\frac{p_{2} q_{2}}{n_{2}}}) \end{equation}
$$
$$
\begin{equation} \frac{(\hat{p}_{1}-\hat{p}_{2})-H_{0}}{\sqrt{\frac{\hat{p}_{1} \hat{q}_{1}}{n_{1}}+\frac{\hat{p_{2}} \hat{q_{2}}}{n_{2}}}}=Z_{\text {calculada }} \sim N(0,1) \end{equation}
$$
\(Pooled\) \(\hat{p}\): Cuando la hipótesis nula considera que las proporción de eventos verdaderos en ambas poblaciones es iguales \(p_{1} = p_{2}\), aun siendo cierta la hipótesis nula, los estimadores muestrales \(\hat{p}_{1}\) y \(\hat{p}_{2}\), raramente lo van a ser debido a la variabilidad.
¿Cuál de los dos emplear entonces? Para facilitar el cálculo, se recomienda con frecuencia emplear lo que se conoce como \(Pooled\) \(\hat{p}\).
$$
\begin{equation} \text { Pooled } \hat{p}=\frac{\text { eventos verdaderos muestra } 1+\text { eventos verdaderos muestra2 }}{n 1+n 2} \end{equation}
$$
De modo que la distribución de la diferencia de las proporciones se aproxima de la siguiente forma:
$$
\begin{equation} (\hat{p}_{1}-\hat{p}_{2}) \sim N(\mu=\text { null value, } S E=\sqrt{\frac{\hat{p}_{\text {pool }}(1-\hat{p}_{p o o l})}{n_{1}}+\frac{\hat{p}_{\text {pool }}(1-\hat{p}_{\text {pool }})}{n_{2}}}. \end{equation}
$$
Nota: La bibliografía parece coincidir en que la pooled \(\hat{p}\) facilita el cálculo pero que si se utiliza la computación es más exacto emplear las \(\hat{p}\) de cada muestra sin combinarlas.
Ejemplo I
Se realiza una encuesta sobre el acoso escolar preguntando a padres y madres sobre sus hijos. Los padres y madres se eligieron aleatoriamente y no están pareados. A la vista de los resultados ¿Existe una diferencia significativa, \(\alpha = 5\%\), entre la opinión de padres y madres sobre sus hijos?
| Respuesta | Madres | Padres |
|---|---|---|
| Si | 61 | 34 |
| No | 61 | 52 |
| Total | 122 | 86 |
1. Hipótesis
\(H_{0}\): No hay diferencia, \(p_{padres}-p_{madres} = 0\).
\(H_{a}\): Sí hay diferencia, \(p_{padres}-p_{madres} \neq 0\), test de dos colas.
2. Estadístico
$$
\begin{equation} \hat{p}_{\text {padres }}-\hat{p}_{\text {madres }}=34 / 86-61 / 122=-0.1047 \end{equation}
$$
3. Condiciones para el TLC
Independencia:
- Dentro de cada muestra: Muestreo aleatorio,
\(n_{1} < 10\%\)población y\(n_{2} < 10\%\)población. - Entre grupos/muestras: Los datos no son pareados.
- Tamaño muestral:
\(122 \times 0.5>=10 \& 122 \times(1-0.5)>=10\)\(86 \times 0.5>=10 \& 90 \times(1-0.0 .5)>=10\)
4. Límite de significancia
$$
\begin{equation} \alpha=0.05 \end{equation}
$$
5. Cálculo de p-value empleando pooled \(\hat{p}\)
Si se cumplen las condiciones para el TLC
$$
\begin{equation} \left(\hat{p}_{1}-\hat{p}_{2}\right) \sim N\left(\mu=\text { null value }, S E=\sqrt{\frac{\hat{p}_{\text {pool }}\left(1-\hat{p}_{\text {pool }}\right)}{n_{1}}+\frac{\hat{p}_{\text {pool }}\left(1-\hat{p}_{\text {pool }}\right)}{n_{2}}}\right. \end{equation}
$$
$$
\begin{equation} \text { pooled } \hat{p}=\frac{61+34}{122+86}=0.4567308 \end{equation}
$$
$$
\begin{equation} S E=\sqrt{\left.\frac{0.46(1-0.46)}{122}+\frac{0.46(1-0.46)}{86}\right)}=0.07017434 \end{equation}
$$
$$
\begin{equation} p_{\text {value }}=2 x p \text { norm }(q=-0.1047, \text { mean }=0, s d=0.07)=0.1347281 \end{equation}
$$
6. Conclusión
\(p-value > \alpha\), no hay evidencias de que las proporciones entre padres y madres difieran de forma significativa para un nivel de significancia del \(5\%\).
Solución con R
La función prop.test() permite comparar si las proporciones de una variable cualitativa con dos niveles son igual entre dos poblaciones, así como generar el intervalo de confianza para la diferencia.
Los argumentos se pueden pasar en forma de vectores dando el número de eventos verdaderos y el tamaño de las muestras o en modo tabla dando el número de positivos y el número de negativos.
prop.test(x = c(61, 34), n = c(122, 86), alternative = "two.side",
conf.level = 0.95, correct = FALSE)
2-sample test for equality of proportions without continuity
correction
data: c(61, 34) out of c(122, 86)
X-squared = 2.2264, df = 1, p-value = 0.1357
alternative hypothesis: two.sided
95 percent confidence interval:
-0.03154603 0.24084835
sample estimates:
prop 1 prop 2
0.5000000 0.3953488
fila1 <- c(61, 61)
fila2 <- c(34, 52)
tabla <- as.table(rbind(fila1, fila2))
dimnames(tabla) = list(Encuestado = c("Padre", "Madre"),
Resultados = c("SI", "NO"))
tabla
Resultados
Encuestado SI NO
Padre 61 61
Madre 34 52
prop.test(x = tabla, alternative = "two.sided", conf.level = 0.95,
correct = FALSE)
2-sample test for equality of proportions without continuity
correction
data: tabla
X-squared = 2.2264, df = 1, p-value = 0.1357
alternative hypothesis: two.sided
95 percent confidence interval:
-0.03154603 0.24084835
sample estimates:
prop 1 prop 2
0.5000000 0.3953488
Conclusión
Se ha mostrado cómo trabajar con variables dicotómicas o de Bernoulli, variables cuyo resultado es verdadero con una probabilidad \(p\).
Referencias
- OpenIntro Statistics: Fourth Edition by David Diez, Mine Çetinkaya-Rundel, Christopher Barr libro
- Handbook of Biological Statistics by John H. McDonald
popular post

Problemas de transporte y asignación
Resumen: Existen dos tipos de problemas especiales en la investigación de operaciones, los problemas de transporte y de asignación.
Leer más
Programación lineal
Resumen: Utilizar R para resolver problemas de programación lineal vinculados a la investigación de operaciones.
Leer más
Programación lineal entera
Resumen: Utilizar R para resolver problemas de programación lineal entera vinculados a la investigación de operaciones.
Leer más