
Prueba de Kaiser-Meyer-Olkin (KMO)
Índice de contenido
Resumen:
La prueba de Kaiser-Meyer-Olkin (KMO) es una medida de la idoneidad de los datos para el análisis factorial. La prueba mide la adecuación del muestreo para cada variable en el modelo y para el modelo completo.
¿Cómo citar el presente artículo?
Romero, J. (1 de enero de 2020). Prueba de Kaiser-Meyer-Olkin (KMO). R.JeshuaRomeroGuadarrama. https://www.r.jeshuaromeroguadarrama.com/es/blog/statistical-tests/kaiser-meyer-olkin-test/.
Prueba de Kaiser-Meyer-Olkin (KMO) by Jeshua Romero Guadarrama, available under Attribution 4.0 International (CC BY 4.0) at https://www.r.jeshuaromeroguadarrama.com/es/blog/statistical-tests/kaiser-meyer-olkin-test/.
Prueba de Kaiser-Meyer-Olkin (KMO) para la adecuación del muestreo
¿Qué es la prueba de Kaiser-Meyer-Olkin (KMO)?
La prueba de Kaiser-Meyer-Olkin (KMO) es una medida de la idoneidad de los datos para el análisis factorial. La prueba mide la adecuación del muestreo para cada variable en el modelo y para el modelo completo. La estadística es una medida de la proporción de varianza entre variables que podrían ser varianza común. Cuanto menor sea la proporción, más adecuados serán los datos para el análisis factorial.
Ahora bien, la prueba de KMO devuelve valores entre \(0\) y \(1\). Una regla general para interpretar la estadística es la siguiente:
- Los valores de KMO entre
\(0.8\)y\(1\)indican que el muestreo es adecuado. - Los valores de KMO inferiores a
\(0.6\)indican que el muestreo no es adecuado y que se deben tomar medidas correctivas. Algunos autores ponen este valor en\(0.5\), así que use su propio juicio para valores entre\(0.5\)y\(0.6\). - Los valores de KMO cercanos a cero significan que existen grandes correlaciones parciales en comparación con la suma de las correlaciones. En otras palabras, existen correlaciones generalizadas que son un gran problema para el análisis factorial.
Como referencia, Kaiser puso los siguientes valores en los resultados:
- 0.00 a 0.49 inaceptable.
- 0.50 a 0.59 miserable.
- 0.60 a 0.69 mediocre.
- 0.70 a 0.79 medio.
- 0.80 a 0.89 meritorio.
- 0.90 a 1.00 maravilloso.
Ejecución de la prueba de Kaiser-Meyer-Olkin (KMO)
La fórmula para la prueba KMO es:
$$ KMO_{j}=\frac{\sum_{i \neq j} r_{i j}^{2}}{\sum_{i \neq j} r_{i j}^{2}+\sum_{i \neq j} u} $$
En cuyo caso:
\(R = [r_{ij}]\)es la matriz de correlación ,\(U = [u_{ij}]\)es la matriz de covarianza parcial,\(\sum\)es la notación de suma (“sumar”).
Esta prueba no suele calcularse a mano (lo más probable es que desee usar software para la prueba), debido a la complejidad.
En \(R\) se hace uso del comando \(KMO(r)\), donde \(r\) es la matriz de correlación que se desea analizar. Encuentre más detalles sobre el comando en R en el sitio web de Personality-Project .
Marco de datos y PCA en R
Se crea el marco de datos socio.data, el cual contiene \(n=12\) instancias y \(p=5\) variables (población, escuela, empleo, servicios, valor de la casa). Se usa el siguiente código \(R\) para cargar el conjunto de datos y realizar el análisis de componentes principales.
Se hace uso de la función data.frame para unir los 5 vectores (variables) y crear el marco de datos:
# Crear los vectores (variables)
Population <- c(5700, 1000, 3400, 3800, 4000, 8200, 1200, 9100, 9900, 9600, 9600, 9400)
School <- c(12.8, 10.9, 8.8, 13.6, 12.8, 8.3, 11.4, 11.5, 12.5, 13.7, 9.6, 11.4)
Employment <- c(2500, 600, 1000, 1700, 1600, 2600, 400, 3300, 3400, 3600, 3300, 4000)
Services <- c(270, 10, 10, 140, 140, 60, 10, 60, 180, 390, 80, 100)
HouseValue <- c(25000, 10000, 9000, 25000, 25000, 12000, 16000, 14000, 18000, 25000, 12000, 13000)
# Crear el marco de datos
socio.data <- data.frame(Population, School, Employment, Services, HouseValue)
print(socio.data)
Population School Employment Services HouseValue
1 5700 12.8 2500 270 25000
2 1000 10.9 600 10 10000
3 3400 8.8 1000 10 9000
4 3800 13.6 1700 140 25000
5 4000 12.8 1600 140 25000
6 8200 8.3 2600 60 12000
7 1200 11.4 400 10 16000
8 9100 11.5 3300 60 14000
9 9900 12.5 3400 180 18000
10 9600 13.7 3600 390 25000
11 9600 9.6 3300 80 12000
12 9400 11.4 4000 100 13000
Ejecutar el PCA usando la función princomp:
socio.pca <- princomp(socio.data, cor = T)
Calcular la proporción de la varianza explicada de los factores:
parte.pca <- socio.pca$sdev^2/sum(socio.pca$sdev^2)*100
print(parte.pca)
Comp.1 Comp.2 Comp.3 Comp.4 Comp.5
57.4662719 35.9332019 4.2967377 1.9986811 0.3051075
Calcular la proporción acumulada de la varianza explicada de los factores:
print(cumsum(parte.pca))
Comp.1 Comp.2 Comp.3 Comp.4 Comp.5
57.46627 93.39947 97.69621 99.69489 100.00000
Representación gráfica del PCA:
biplot(socio.pca)
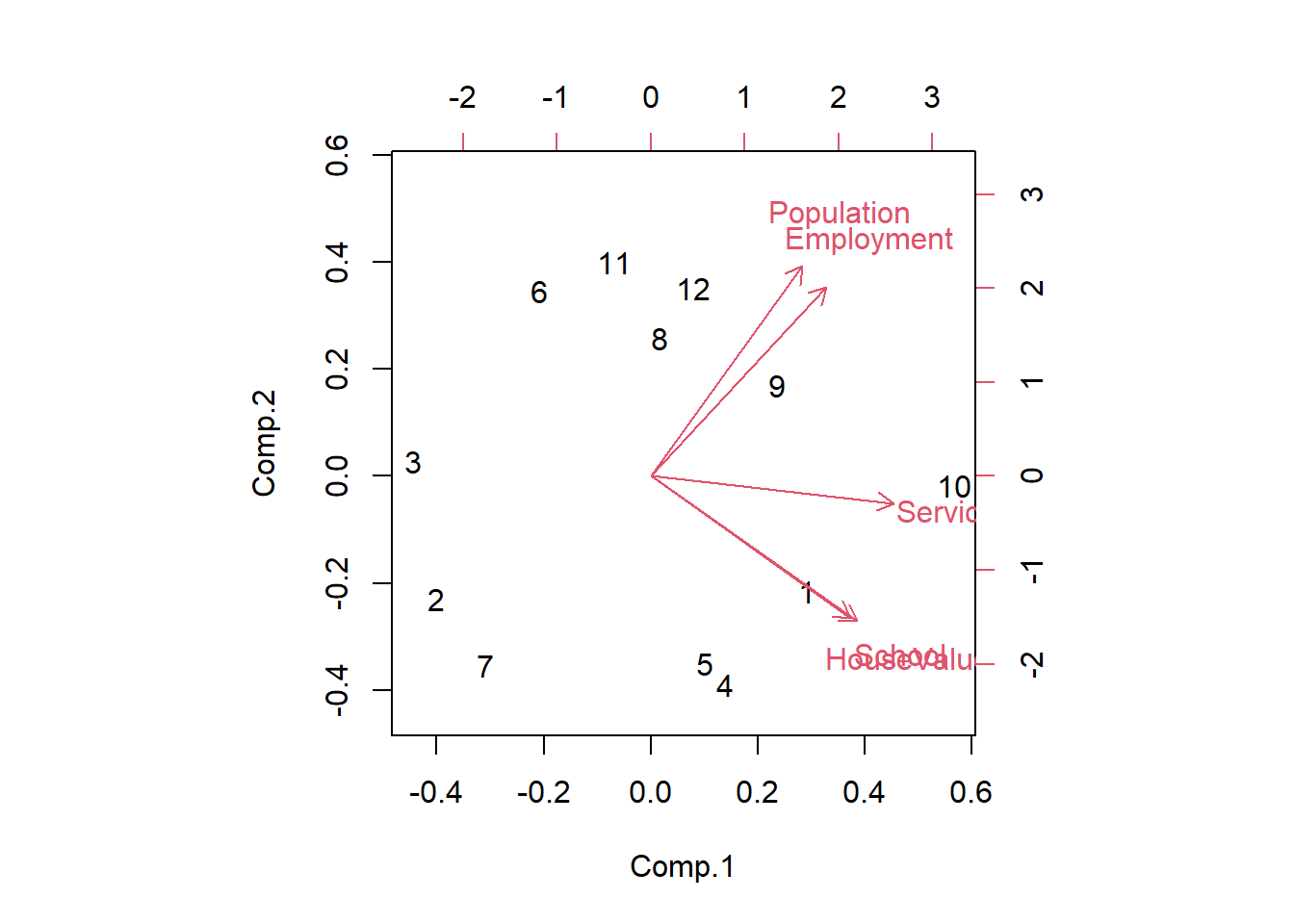
Los dos primeros factores representan el \(93.4\%\) de la varianza disponible. Se puede considerar que se teine una imagen precisa de la información disponible en los datos de estos factores.
Prueba de KMO Medida de Adecuación de Muestreo (MSA) en R
El índice KMO comprueba si se pueden factorizar eficientemente las variables originales.
La matriz de correlación es siempre el punto de partida. Se sabe que las variables están más o menos correlacionadas, pero la correlación entre dos variables puede verse influenciada por las demás. Entonces, usando la correlación parcial para medir la relación entre dos variables, eliminando el efecto de las variables restantes. El índice KMO compara los valores de las correlaciones entre variables y los de las correlaciones parciales:
- Si el índice KMO es alto ($\approx 1$), el PCA puede actuar de manera eficiente.
- Si el índice KMO es bajo ($\approx 0$), el PCA no es relevante.
Algunas referencias dan una tabla para la interpretación del valor del índice KMO obtenido sobre un conjunto de datos.
Cálculo de las correlaciones entre las variables
Calcular la matriz de correlación en R:
R <- cor(socio.data)
print(R)
Population School Employment Services HouseValue
Population 1.00000000 0.00975059 0.9724483 0.4388708 0.02241157
School 0.00975059 1.00000000 0.1542838 0.6914082 0.86307009
Employment 0.97244826 0.15428378 1.0000000 0.5147184 0.12192599
Services 0.43887083 0.69140824 0.5147184 1.0000000 0.77765425
HouseValue 0.02241157 0.86307009 0.1219260 0.7776543 1.00000000
Algunas variables están correlacionadas (por ejemplo, población y empleo: \(0.97\) o escuela y valor de la vivienda: \(0.86\)). Aquí, el objetivo es solo obtener una impresión general sobre la redundancia entre las variables. Ahora bien, se debe confirmar con un riguroso procedimiento estadístico.
Matriz de correlación parcial
La matriz de correlación parcial se puede obtener a partir de la matriz de correlación. Se calcula la inversa de esta última \(R^{-1}=(v_{ij})\):
invR <- solve(R)
print(invR)
Population School Employment Services HouseValue
Population 31.838614 7.2900372 -31.2039095 -1.1716282 -2.289677
School 7.290037 5.6269914 -7.3470098 -0.2560012 -3.924997
Employment -31.203909 -7.3470098 32.4473253 -0.8231689 3.724281
Services -1.171628 -0.2560012 -0.8231689 4.6668869 -3.281654
HouseValue -2.289677 -3.9249973 3.7242815 -3.2816538 6.536768
Se calcula la correlación parcial \(A=(a_{ij})\) de la siguiente manera:
$$ a_{i j}=-\frac{v_{i j}}{\sqrt{v_{i i} \times v_{j j}}} $$
Aquí hay un programa muy simple para este cálculo en R:
# Matriz de correlación parcial
A <- matrix(1, nrow(invR), ncol(invR))
for (i in 1:nrow(invR)){
for (j in (i):ncol(invR)){
# Sobre la diagonal
A[i,j] <- -invR[i,j]/sqrt(invR[i,i]*invR[j,j])
# Debajo de la diagonal
A[j,i] <- A[i,j]
}
}
colnames(A) <- colnames(socio.data)
rownames(A) <- colnames(socio.data)
print(A)
Population School Employment Services HouseValue
Population -1.00000000 -0.54464628 0.9708284 0.09611676 0.1587141
School -0.54464628 -1.00000000 0.5437297 0.04995629 0.6471720
Employment 0.97082842 0.54372968 -1.0000000 0.06689380 -0.2557240
Services 0.09611676 0.04995629 0.0668938 -1.00000000 0.5941520
HouseValue 0.15871414 0.64717195 -0.2557240 0.59415202 -1.0000000
Índice general de KMO
El índice KMO general se calcula de la siguiente manera.
$$ KMO=\frac{\sum_{i} \sum_{j \neq i} r_{i j}^{2}}{\sum_{i} \sum_{j \neq i} r_{i j}^{2}+\sum_{i} \sum_{j \neq i} a_{i j}^{2}} $$
Si la correlación parcial es cercana a cero, el PCA puede realizar eficientemente la factorización porque las variables están altamente relacionadas: \(\mathrm{KMO} \approx 1\).
Se realiza el cálculo del programa en R:
kmo.num <- sum(R^2) - sum(diag(R^2))
kmo.denom <- kmo.num + (sum(A^2) - sum(diag(A^2)))
kmo <- kmo.num/kmo.denom
print(kmo)
[1] 0.5753676
Con el valor \(KMO = 0.575\), el grado de varianza común en el conjunto de datos es bastante “mediocre”. Por lo tanto, se recomienda agregar variables en el análisis para obtener resultados más confiables.
Una regla comúnmente utilizada es que debe haber al menos tres variables por factor. Para el presente conjunto de datos, solo se tiene \(p=5\) variables para \(k=2\) factores.
Índice KMO por variable
Se puede calcular un índice KMO por variable para detectar aquellas que no están relacionadas con las demás:
$$ KMO_{j}=\frac{\sum_{i \neq j} r_{i j}^{2}}{\sum_{i \neq j} r_{i j}^{2}+\sum_{i \neq j} a_{i j}^{2}} $$
Se realiza el cálculo del programa en R:
# KMO por variable
for (j in 1:ncol(socio.data)){
kmo_j.num <- sum(R[,j]^2) - R[j,j]^2
kmo_j.denom <- kmo_j.num + (sum(A[,j]^2) - A[j,j]^2)
kmo_j <- kmo_j.num/kmo_j.denom
print(paste(colnames(socio.data)[j],"=",kmo_j))
}
[1] "Population = 0.472078968813805"
[1] "School = 0.551588388856226"
[1] "Employment = 0.488511365390876"
[1] "Services = 0.806643649483337"
[1] "HouseValue = 0.61281377023744"
Las variables “Población” ($0.472$) y “Empleo” ($0.488$) parecen problemáticas. Esto se debe a que están altamente correlacionadas entre sí ($r=0.94$), pero no correlacionadas con las otras variables (la correlación parcial también es alta, \(v=0.97\)). No es realmente un problema de hecho. Estas variables no están relacionadas con las demás (lo que determina el primer factor), ellas definen el segundo factor del PCA.
Conclusión
El índice KMO permite detectar si se puede o no resumir la información proporcionada por las variables iniciales en unos pocos factores. No obstante, no da indicaciones sobre el número apropiado de factores. En este contexto, he mostrado cómo calcularlos con un programa escrito en R. Finalmente, resulta importante mencionar que los cálculos son factibles solo si la matriz de correlación es invertible.
Referencias
- Esquivar, Y. (2008). La Enciclopedia Concisa de Estadística. Saltador.
- Gonick, L. (1993). La guía de dibujos animados de estadísticas. Harper Perennial.
- Klein, G. (2013). La caricatura: Introducción a la estadística. Colina y Wamg.
- Snedecor, George W. y Cochran, William G. (1989), Métodos estadísticos, octava edición, Iowa State University Press.
- Vogt, WP (2005). Diccionario de estadística y metodología: Una guía no técnica para las ciencias sociales. SABIO.
popular post

Problemas de transporte y asignación
Resumen: Existen dos tipos de problemas especiales en la investigación de operaciones, los problemas de transporte y de asignación.
Leer más
Programación lineal
Resumen: Utilizar R para resolver problemas de programación lineal vinculados a la investigación de operaciones.
Leer más
Programación lineal entera
Resumen: Utilizar R para resolver problemas de programación lineal entera vinculados a la investigación de operaciones.
Leer más