
Prueba T en R
Index du contenu
Resumen:
Prueba T para comparar medias poblacionales independientes y dependientes (pareadas).
¿Cómo citar el presente artículo?
Romero, J. (Enero 1, 2019). Prueba T en R. R.JeshuaRomeroGuadarrama. https://www.r.jeshuaromeroguadarrama.com/es/blog/applied-statistics/t-test/.
Prueba T en R by Jeshua Romero Guadarrama, available under Attribution 4.0 International (CC BY 4.0) at https://www.r.jeshuaromeroguadarrama.com/es/blog/applied-statistics/t-test/.
Prueba T: Comparación de medias poblacionales independientes
Introducción
Una de las opciones cuando se quiere comparar una variable continua entre dos grupos consiste en comparar los resultados promedio obtenidos para cada uno. El hecho de que los valores promedio de cada grupo no sean iguales no implica que haya evidencias de una diferencia significativa. Dado que cada grupo tiene su propia variabilidad, aunque el tratamiento no sea eficaz, las medias muestrales no tienen por qué ser exactas.
Para estudiar si la diferencia observada entre las medias de dos grupos es significativa, se puede recurrir a métodos paramétricos como el basado en Z-scores o en la distribución T-student. En ambos casos, se pueden calcular tanto intervalos de confianza para saber entre que valores se encuentra la diferencia real de las medias poblacionales o test de hipótesis para determinar si la diferencia es significativa.
La distribución T-student se asemeja en gran medida a la distribución normal. Tiene como parámetros la media, la varianza y además incorpora a través de los grados de libertad una modificación que permite flexibilizar las colas en función del tamaño que tenga la muestra. A medida que se reduce el tamaño muestral, la probabilidad acumulada en las colas aumenta, siendo así menos estricta de lo cabría esperar en una distribución normal. Una distribución T-student con 30 o más grados de libertad es prácticamente igual a una distribución normal.
El número de grados de libertad de la distribución T-student se calcula:
- Para estudiar una sola muestra: df= tamaño de la muestra −1
- Cuando se comparan dos muestras: Existen varios métodos, uno de los utilizados es emplear los grados de libertad de la muestra de menor tamaño mínimo ((n1−1),(n2−1)). En los programas informáticos se emplean métodos para ajustar de forma más precisa los grados de libertad.
Condiciones de una prueba T para muestras independientes
Las condiciones para calcular intervalos de confianza o aplicar un test de hipótesis basados en la distribución T−student son las mismas que para el teorema del límite central.
- Independencia: Las observaciones tienen que ser independientes unas de las otras. Para ello el muestreo debe ser aleatorio y el tamaño de la muestra inferior al 10% de la población.
- Normalidad: Las poblaciones que se comparan tienen que distribuirse de forma normal. A pesar de que la condición de normalidad recae sobre las poblaciones, normalmente no se dispone de información sobre ellas por lo que las muestras (dado que son reflejo de la población) tiene que distribuirse de forma aproximadamente normal. En caso de cierta asimetría los t-test son considerablemente robustos cuando el tamaño de las muestras es mayor o igual a 30.
- Igualdad de varianza (homocedasticidad): La varianza de ambas poblaciones comparadas debe de ser igual. Tal como ocurre con la condición de normalidad, si no se dispone de información de las poblaciones, esta condición se ha de asumir a partir de las muestras. En caso de no cumplirse esta condición se puede emplear un WelchTwoSampleT−test. Esta corrección se incorpora a través de los grados de libertad permitiendo compensar la diferencia de varianzas pero con el inconveniente de que pierde precisión. El número de grados de libertad de un WelchTwoSampleT−test viene dado por la siguiente función:
f=(ˆS21n1+ˆS22n2)21n1+1(ˆS21n1)2+1n2+1(ˆS22n2)2−2
Si las condiciones se cumplen se puede considerar que el parámetro estimado, en este caso la diferencia de medias muestrales (ˉX1−ˉX2) sigue una distribución T−student (\text{grados de libertad}, mean=parámetro estimado, sd=SE)
El error estandár (SE) de una distribución T-student para comparar medias se define como la raíz cuadrada de la suma de las desviaciones típicas muestrales corregidas de cada grupo al cuadrado, divididas por el tamaño de cada muestra.
SE=√ˆS21n1+ˆS22n2
El proceso a seguir para calcular intervalos de confianza o test de hipótesis es el mismo que el seguido en el modelo Normal. La única diferencia es que en lugar de emplear Z-scores (cuantiles de la distribución normal) se emplean los T-scores (cuantiles de la distribución t-student).
Intervalo de confianza
El intervalo de confianza de la diferencia de medias independientes para un nivel de confianza de 1−α tiene la siguiente estructura:
[(ˉX1−ˉX2)±tdf,1−α/2∗√.ˆS21n1+ˆS22n2].
El valor t depende del porcentaje de seguridad del intervalo de confianza que se quiera obtener. Se define como el valor (cuantil) para el cual en una distribución de student, con unos determinados grados de libertad, un porcentaje igual al porcentaje de confianza del intervalo queda comprendido entre el valor −t y el valor +t buscado.
Supóngase que se busca el valor t para un intervalo de confianza del 95% en una distribución t−student con 15 grados de libertad:

El valor t puede encontrarse en tablas tabuladas o mediante programas informáticos, en R el valor t para un determinado intervalo de confianza y grados de libertad se puede obtener con la función qt().
En este contexto, se tiene que t = qt(p = confianza del intervalo + (1-confianza intervalo)/2, df= , lower.tail = TRUE).
qt(p = 0.95 + 0.05/2, df = 15, lower.tail = TRUE)
[1] 2.13145
Test de hipótesis
Los pasos a seguir para realizar un t-test de medias independientes son:
- Establecer las hipótesis.
- Calcular el estadístico (parámetro estimado) que se va a emplear.
- Determinar el tipo de test, una o dos colas.
- Determinar el nivel de significancia α.
- Cálculo de p−value y comparación con el nivel de significancia establecido.
- Cálculo del tamaño del efecto (opcional pero recomendado).
- Conclusiones.
1. Establecer las hipótesis
Hipótesis nula (H0): Por lo general es la hipótesis escéptica, la que considera que no hay diferencia o cambio. Suele contener en su definición el símbolo =.
En el caso de comparar dos medias independientes la hipótesis nula considera que μ1=μ2.
Hipótesis alternativa (HA): Considera que el valor real de la media poblacional es mayor, menor o distinto del valor que establece la Ho. Suele contener los símbolos >, <, ≠.
En el caso de comparar dos medias independientes la hipótesis alternativa considera que μ1≠μ2.
2. Calcular el estadístico (parámetro estimado)
El estadístico es el valor que se calcula a partir de la muestra y que se quiere extrapolar a la población de origen.
En este caso es la diferencia de las medias muestrales (ˉX1−ˉX2)
3. Determinar el tipo de test, una o dos colas
Los test de hipótesis pueden ser de una cola o de dos colas:
- Si la hipótesis alternativa emplea “>” o “<” se trata de un test de una cola, en el que solo se analizan desviaciones en un sentido.
- Si la hipótesis alternativa es del tipo “diferente de” se trata de un test de dos colas, en el que se analizan posibles desviaciones en las dos direcciones.
Solo se emplean test de una cola cuando se sabe con seguridad que las desviaciones de interés son en un sentido y únicamente si se ha determinado antes de observar la muestra, no a posteriori.
4. Determinar el nivel de significancia α
El nivel de significancia α determina la probabilidad de error que se quiere asumir a la hora de rechazar la hipótesis nula. Se emplea como punto de referencia para determinar si el valor de p−value obtenido en el test de hipótesis es suficientemente bajo como para considerar significativas las diferencias observadas y por lo tanto rechazar H0. A menor valor de α, menor probabilidad de rechazar la hipótesis nula. Por ejemplo, si se considera α=0.05, se rechazará la hipótesis nula en favor de la hipótesis alternativa si el p−value obtenido es menor que 0.05, y se tendrá una probabilidad del 5% de haber rechazado H0 cuando realmente es cierta. En nivel de significancia debe establecerse en función de que error sea más costoso:
- Error tipo I: Error de rechazar la H0 cuando realmente es cierta
- Error tipo II: Error de considerar como cierta H0 cuando realmente es falsa.
5. Cálculo de p-value y comparación con el nivel de significancia
Si las condiciones mencionadas previamente se cumplen, se puede considerar que:
T=(ˉX1−ˉX2)−(μ1−μ2)SE∼t(df)
Teniendo en cuenta que:
SE=√ˆS21n1+ˆS22n2
ˆS es la cuasidesviación típica muestral o desviación típica muestral corregida:
pvalue=P(|Tcalculada |>=tdf,1−α/2)
6. Tamaño del efecto
El tamaño del efecto o también llamado effect size es la diferencia neta observada entre los grupos de un estudio. No se trata de una medida de inferencia estadística ya que no se pretende identificar si las poblaciones son significativamente diferentes, sino que simplemente indica la diferencia observada entre muestras, independientemente de la varianza que tengan. Se trata de un parámetro que siempre debe acompañar a los p−values, ya que un p−value solo indica si hay evidencias significativas para rechazar la hipótesis nula pero no dice nada de si la diferencia es importante o práctica. Esto último se averigua mediante el tamaño del efecto.
En el caso de los t−test de medias independientes, existen dos medidas posibles del tamaño del efecto:
- La d de Cohen y la r de Pearson. Ambas son equivalentes y pueden transformarse de una a otra. Cada una de estas medidas tiene unas magnitudes recomendadas para considerar el tamaño del efecto como pequeño, mediano o grande.
- La función
cohen.d()del paqueteeffsizepermite calcular el tamaño del efecto de la diferencia de medias independientes.
D de Cohen para prueba T independiente:
d=∣ diferencia de medias entre los grupos ∣sd
Existen dos formas distintas se utilizan para calcular la sd conjunta de ambas muestras:
sd=√(n−1)sd21+(n−2)sd22)n1+n2−2
Los límites más utilizados para clasificar el tamaño del efecto con d−Cohen son:
- d≤0.2 pequeño
- d≥0.5 mediano
- d=0.8 grande
R de Pearson para prueba T independiente:
r=√t2(t2+gl)
- t= estadístico t obtenido en el test
- gl= grados de libertad del test
Los límites más utilizados para clasificar el tamaño del efecto con r son:
- d≤0.1 pequeño
- d≥0.3 mediano
- d=0.5 grande
7. Interpretación de los resultados
Si el p−value es menor que el valor de α seleccionado, existen evidencias suficientes para rechaza H0 en favor de Ha.
Ejemplos
Ejemplo I: Solución manual
Se quiere estudiar el efecto de un fármaco sobre el apetito, para ello se mide la ingesta de comida (gramos) de dos grupos de personas seleccionadas al azar. En vista de los resultados ¿Se puede considerar que el fármaco funciona para un nivel de significancia del 5%?
| Grupo | Media muestral | ˆS | n |
|---|---|---|---|
| control | 52.1 | 45.1 | 22 |
| tratamiento | 27.1 | 26.4 | 22 |
1. Hipótesis
H0: No hay diferencia entre las medias, media control − media tratamiento =0
Ha: Sí hay diferencia entre las medias, media control − media tratamiento ≠0
2. Parámetro estimado (estadístico)
media control − media tratamiento =52.1−27.1=25
3. Modelo del test
t−student, p−value test 2 colas
4. Condiciones para comparar dos medias independientes
En este ejemplo no se dispone de los datos, por lo que se asume que se cumplen las condiciones.
5. Nivel de significancia
α=0.05
6. Cálculo de p-value
Parámetro estimado =25 Grados de libertad = min (22−1,22−1)=21
SE(media control − media tratamiento) =√ˆS2control ncontrol +ˆS2tratamiento ntratamiento
sqrt((45.1^2 / 22) + (26.4^2 / 22))
[1] 11.14159
T=(ˉX1−ˉX2)−(μ1−μ2)SE=25−011.14=2.24
pt(q = -2.24, df = 21) + (1 - pt(q = 2.24, df = 21))
[1] 0.03603696
7. Tamaño del efecto
sd=√.(22−1)45.12+(22−2)26.42)22+22−2=36.73
8. Conclusión
En este caso, dado p−value <α, hay evidencias significativas para rechazar H0 en favor de Ha, siendo el tamaño del efecto (d-Cohen) medio. Se pude considerar que el tratamiento funciona.
Ejemplo II: Solución mediante R
El datset births del paquete openintro contiene información sobre 150 nacimientos junto con información de las madres. Se quiere determinar si existen evidencias significativas de que el peso de los recién nacidos cuyas madres fuman (f) difiere de aquellos cuyas madres no fuman (nf).
library(openintro)
library(tidyverse)
data(births)
head(births, 4)
# A tibble: 4 x 9
f_age m_age weeks premature visits gained weight sex_baby smoke
<int> <int> <int> <fct> <int> <int> <dbl> <fct> <fct>
1 31 30 39 full term 13 1 6.88 male smoker
2 34 36 39 full term 5 35 7.69 male nonsmoker
3 36 35 40 full term 12 29 8.88 male nonsmoker
4 41 40 40 full term 13 30 9 female nonsmoker
1. Hipótesis
H0: No hay diferencia entre las medias poblacionales: μ(nf)−μ(f)=0.
Ha: Si hay diferencia entre las medias poblacionales: μ(nf)−μ(f)≠0.
2. Parámetro estimado (estadístico)
Diferencia entre las medias muestrales:
smoker <- births %>% filter(smoke == "smoker") %>% pull(weight)
nonsmoker <- births %>% filter(smoke == "nonsmoker") %>% pull(weight)
mean(nonsmoker) - mean(smoker)
[1] 0.4005
3. Condiciones para aplicar un t-test
Independencia: Se trata de un muestreo aleatorio donde el tamaño de las muestras no supera el 10% de todos los nacimientos en carolina del norte. Se puede afirmar que los eventos son independientes.
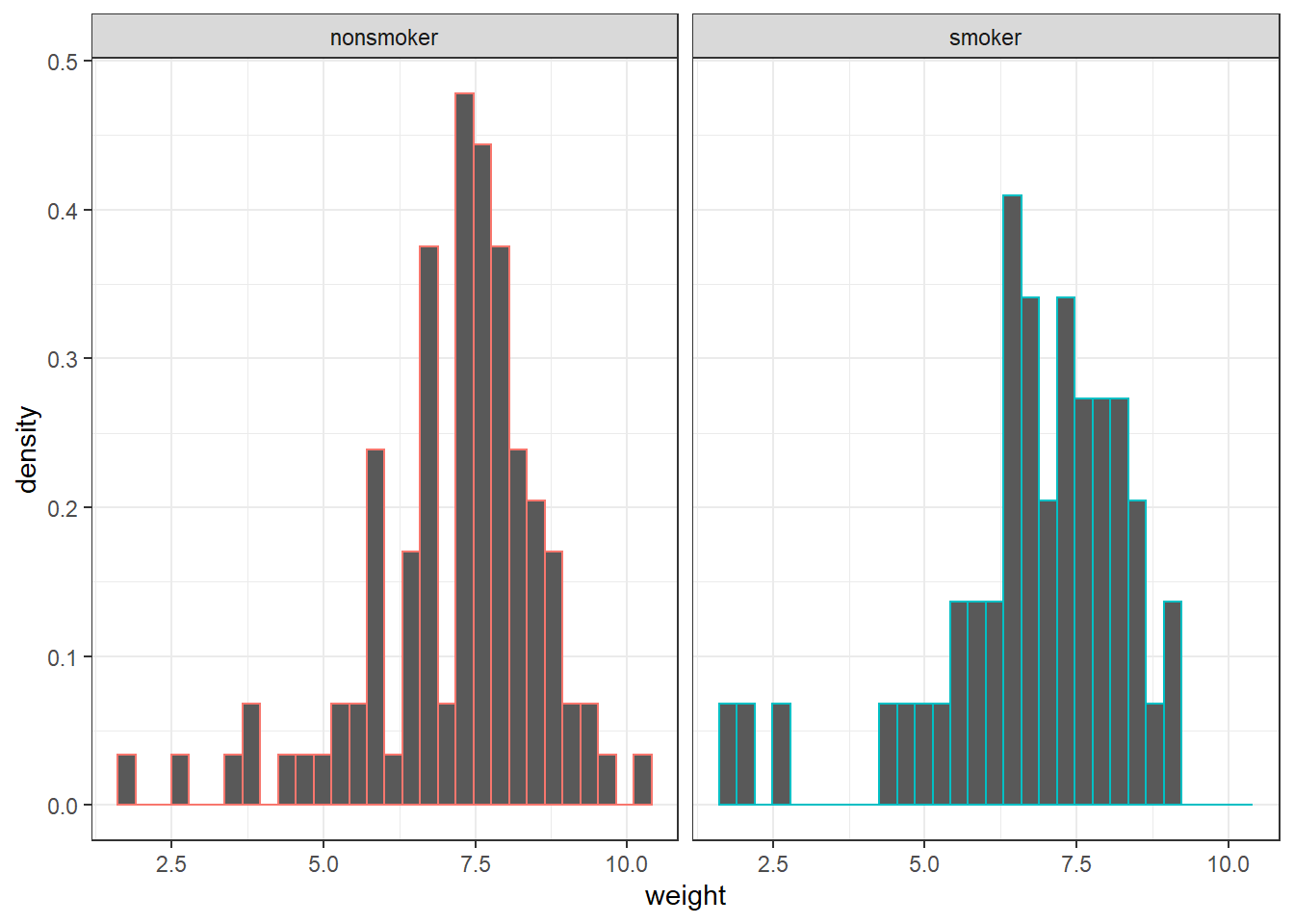
Normalidad:
ggplot(births,aes(x = weight)) +
geom_histogram(aes(y = ..density.., colour = smoke)) +
facet_grid(.~ smoke) +
theme_bw() + theme(legend.position = "none")
par(mar = c(2, 2, 2, 2))
par(mfrow = c(1, 2))
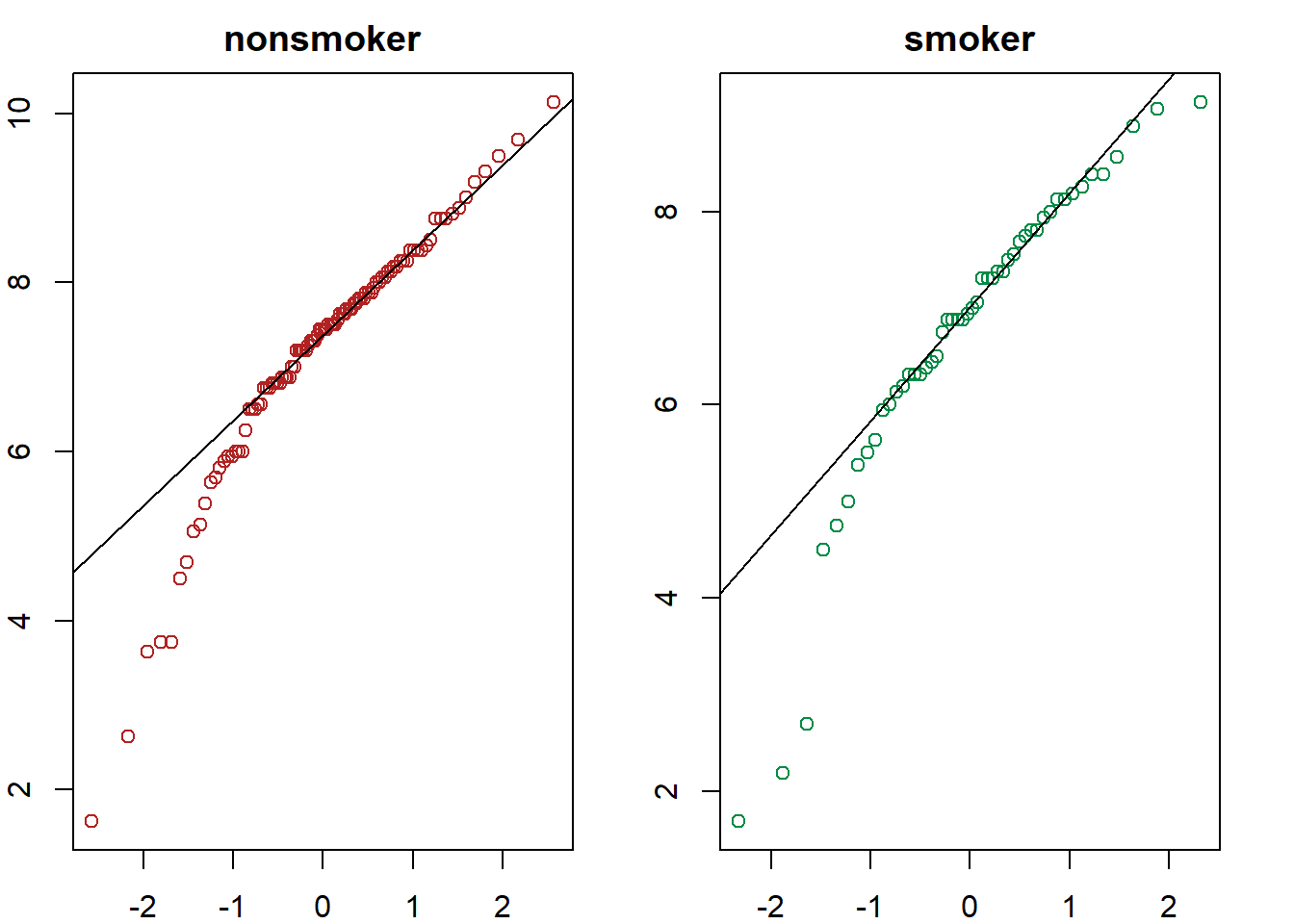
qqnorm(nonsmoker, xlab = "", ylab = "",
main = "nonsmoker", col = "firebrick")
qqline(nonsmoker)
qqnorm(smoker, xlab = "", ylab = "",
main = "smoker", col = "springgreen4")
qqline(smoker)
shapiro.test(smoker)
Shapiro-Wilk normality test
data: smoker
W = 0.89491, p-value = 0.0003276
shapiro.test(nonsmoker)
Shapiro-Wilk normality test
data: nonsmoker
W = 0.92374, p-value = 2.234e-05
Los gráficos qqnorm muestran asimetría hacia la izquierda y los test encuentran evidencias significativas de que los datos no proceden de poblaciones con distribución normal.
Sin embargo, dado que el tamaño de cada grupo es mayor que 30 se puede considerar que el t−test sigue siendo suficientemente robusto, aunque es necesario mencionarlo en las conclusiones.
Un test no paramétrico basado en la mediana (Mann−Withney−Wilcoxon test) o un test de Bootstraping serían más adecuados. Otra opción sería estudiar si los datos anómalos son excepciones que se pueden excluir del análisis.
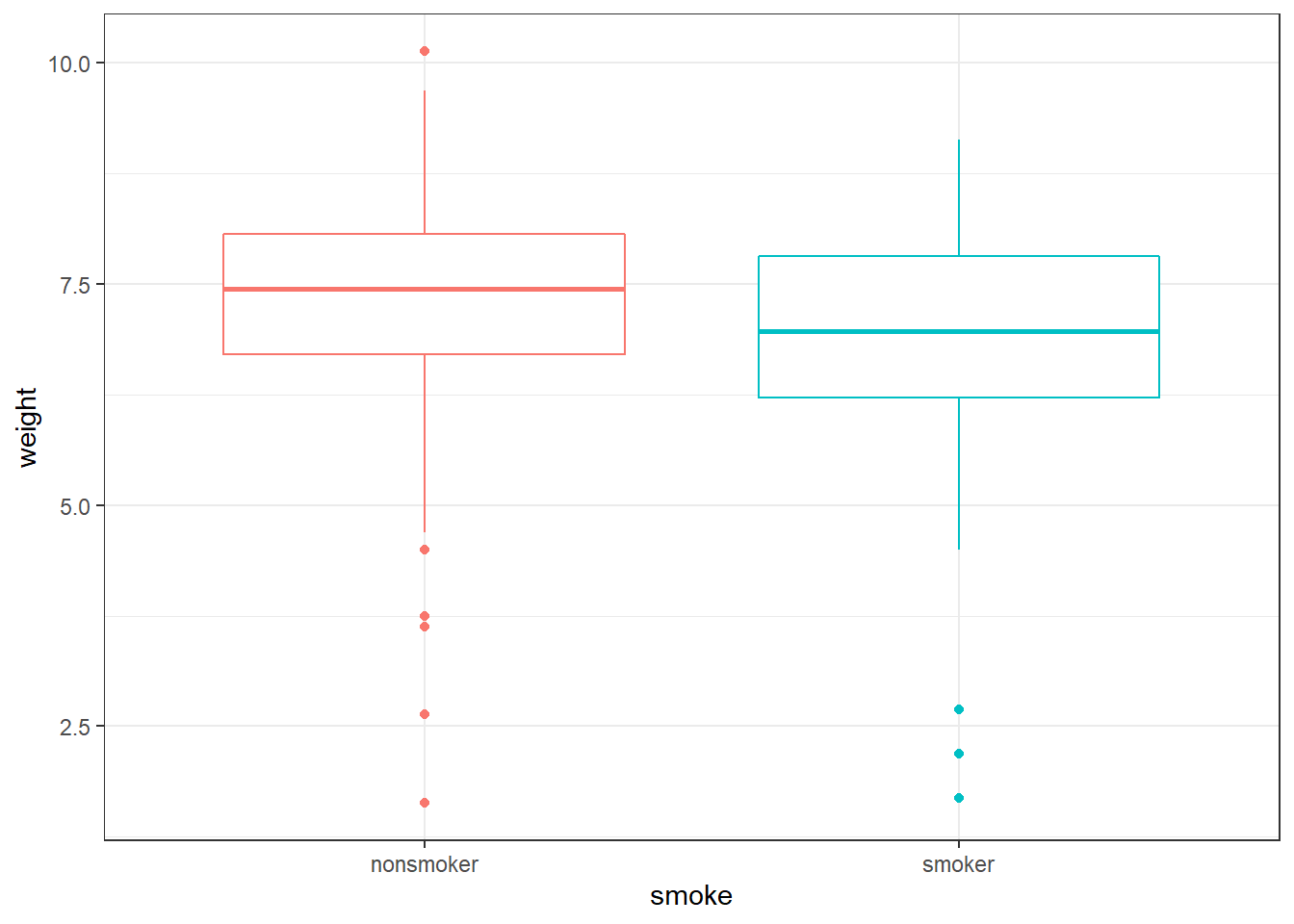
Igualdad de varianza:
Existen varios test que permiten comparar varianzas.
Dado que no se cumple el criterio de normalidad, uno de los recomendados es el test Leven o el test no paramétrico de Fligner−Killeen (ambos basados en la mediana).
ggplot(data = births) +
geom_boxplot(aes(x = smoke, y = weight, colour = smoke)) +
theme_bw() + theme(legend.position = "none")
require(car)
fligner.test(weight ~ smoke, data = births)
Fligner-Killeen test of homogeneity of variances
data: weight by smoke
Fligner-Killeen:med chi-squared = 0.56858, df = 1, p-value = 0.4508
leveneTest(weight ~ smoke, data = births, center = "median")
Levene's Test for Homogeneity of Variance (center = "median")
Df F value Pr(>F)
group 1 0.4442 0.5062
148
Ninguno de los dos test encuentra evidencias significativas (para α=0.05) de que las variancias sean distintas entre ambas poblaciones.
Si las varianzas no fuesen iguales se tendría que realizar el t−test con la corrección de Welch.
4. Nivel de significancia
α=0.05
5. Cálculo de p-value
R tiene una función integrada que permite realizar t−test para una o dos muestras, tanto con corrección (en caso de que las varianzas no sean iguales) como sin ella.
Esta función devuelve tanto el p−value del test como el intervalo de confianza para la verdadera diferencia de medias.
t.test(
x = smoker,
y = nonsmoker,
alternative = "two.sided",
mu = 0,
var.equal = TRUE,
conf.level = 0.95
)
Two Sample t-test
data: smoker and nonsmoker
t = -1.5517, df = 148, p-value = 0.1229
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-0.9105531 0.1095531
sample estimates:
mean of x mean of y
6.7790 7.1795
6. Cálculo tamaño de efecto
library(effsize)
cohen.d(formula = weight ~ smoke, data = births, paired = FALSE)
Cohen's d
d estimate: 0.2687581 (small)
95 percent confidence interval:
lower upper
-0.07488708 0.61240332
7. Conclusión
Dado que p−value (0.1229) es mayor que α (0.05), no se dispone de evidencia suficiente para considerar que existe una diferencia entre el peso promedio de niños nacidos de madres fumadores y el de madres no fumadoras.
El tamaño de efecto medido por d−Cohen es pequeño (0.27).
T-test: Comparación de medias poblacionales dependientes (pareadas)
Introducción
Dos medias son dependientes o pareadas cuando proceden de grupos o muestras dependientes, esto es, cuando existe una relación entre las observaciones de las muestras. Este escenario ocurre a menudo cuando los resultados se generan a partir de los mismos individuos bajo dos condiciones distintas.
Por ejemplo, si se quiere comprobar el resultado de dos tipos de exámenes (lectura y escritura) sobre los alumnos de un colegio, es de esperar que alumnos que obtienen una alta calificación en un examen también lo hagan en el otro. Otro caso similar son los estudios médicos en los que se compara una característica pre-tratamiento y post-tratamiento sobre los mismos individuos.
Para poder determinar si los individuos (observaciones) han sufrido una diferencia significativa entre las condiciones X e Y, se calcula para cada uno de ellos el cambio en la magnitud estudiada di=xi−yi.
A pesar de que no exista diferencia entre las dos condiciones (por ejemplo, que la presión sanguínea es igual antes y después del tratamiento), al calcular la diferencia entre el antes y después de cada individuo probablemente el valor no sea exactamente cero, ya que debido a la variabilidad se van a producir desviaciones por encima y por debajo de cero.
Sin embargo, el promedio de todas las diferencias tenderá a cero (compensación de desviaciones). Es este promedio (μdiferencia) el que se estudia a través del siguiente estadístico muestral:
ˉd=∑ni=1(xantes −xdespués )n
Determinando si el promedio de las diferencias observado en la muestra se aleja lo suficiente del valor nulo (cero, en caso de considerar que ambas medias son iguales) como para aceptar que el valor medio de ambos grupos no es el mismo.
Los test dependientes o pareados tienen la ventaja frente a los independientes de que se puede controlar mejor la variación no sistemática (la producida por variables no contempladas en el estudio) ya que se bloquean al estar examinado los mismos individuos dos veces, no dos grupos de individuos distintos.
Condiciones para un t-test de muestras dependientes
Normalidad: Solo es aplicable si se puede asumir que las dos poblaciones que se comparan se distribuyen de forma normal. La normalidad se tiene que cumplir en las poblaciones. Sin embargo, cuando no se dispone de información sobre las poblaciones, la única forma de estimar su distribución es a partir de las muestras.
Varianza: No es necesario que las variancias de ambos grupos sean iguales (homocedasticidad no necesaria).
Si las condiciones mencionadas se cumplen, se puede considerar que:
d∼N(μd,σ2d)
Como en la mayoría de casos en los que se aplica inferencia estadística se desconoce μ у σ, se emplean estimadores obtenidos a partir de las muestras:
ˉd∼N(ˉd,ˆS2d)
Hipótesis
H0: no hay diferencia entre las medias, el promedio de las diferencias es 0 (μd=0) o bien es un valor determinado (Δ).
Ha: sí hay diferencia entre las variables, (μd≠0) o bien la diferencia es distinta al valor establecido en la hipótesis nula (μd≠Δ).
El resto del proceso es el mismo que el seguido en un t−test para medias independientes:
Tcalculado =ˉd− valor H0SE
Siendo el SE del promedio de las diferencias igual a la cuasidesviación típica muestral dividida entre la raíz cuadrada del número de pares de datos:
ˆSd√n
Ejemplos
Ejemplo I: Solución manual
Un equipo de atletismo ha decidido contratar a un nuevo entrenador. Para decidir si al cabo de un año mantienen su contrato se selecciona aleatoriamente a 10 miembros del equipo y se cronometran sus tiempos en 100 metros lisos al inicio del año, al final del año se volverá a cronometrar a esos mismos 10 corredores. En vista de los datos obtenidos ¿Hay diferencia significativa entre el rendimiento de los corredores tras un año de entrenar con el nuevo instructor?
Se trata de un caso de estudio en el que las mediciones se realizan sobre los mismos individuos bajo dos condiciones distintas, se trata de datos pareados.
datos <- data.frame(
corredor = c(1:10),
antes = c(12.9, 13.5, 12.8, 15.6, 17.2, 19.2, 12.6, 15.3, 14.4, 11.3),
despues = c(12.7, 13.6, 12.0, 15.2, 16.8, 20.0, 12.0, 15.9, 16.0, 11.1)
)
head(datos, 4)
corredor antes despues
1 1 12.9 12.7
2 2 13.5 13.6
3 3 12.8 12.0
4 4 15.6 15.2
Al tratarse de datos pareados, interesa conocer la diferencia en cada par de observaciones.
diferencia <- datos$antes - datos$despues
datos <- cbind(datos, diferencia)
head(datos,4)
corredor antes despues diferencia
1 1 12.9 12.7 0.2
2 2 13.5 13.6 -0.1
3 3 12.8 12.0 0.8
4 4 15.6 15.2 0.4
colMeans(datos[,-1])
antes despues diferencia
14.48 14.53 -0.05
1. Establecer las hipótesis
H0: no hay diferencia entre el tiempo medio de los corredores al inicio y al final del año. El promedio de las diferencias es cero (μd=0).
Ha: sí hay diferencia entre el tiempo medio de los corredores al inicio y al final del año. El promedio de las diferencias no es cero (μd≠0).
2. Establecer el estadístico (parámetro estimado) que se va a emplear
El estadístico es el valor que se calcula a partir de la muestra y que se quiere extrapolar a la población de origen. En este caso es el promedio de las diferencias entre cada par de observaciones ˉd=−0.5.
3. Determinar el tipo de test, una o dos colas
Los test de hipótesis pueden ser de una cola o de dos colas. Si la hipótesis alternativa emplea “>” o “<” se trata de un test de una cola, en el que solo se analizan desviaciones en un sentido. Si se la hipótesis alternativa es del tipo “diferente de” se trata de un test de dos colas, en el que se analizan posibles desviaciones en las dos direcciones. Solo se emplean test de una cola cuando se sabe con seguridad que las desviaciones de interés son en un sentido y únicamente si se ha determinado antes de observar la muestra, no a posteriori.
En este caso solo se va a contratar al entrenador si el rendimiento ha mejorado, por lo que la hipótesis alternativa sería más exacta si se considera como (μd>0), es decir, que la media de tiempos al final del año es menor que al inicio.
4. Determinar el nivel de significancia α
α=0.05
El nivel de significancia α determina la probabilidad de error que se quiere asumir a la hora de rechazar la hipótesis nula.
Se emplea como punto de referencia para determinar si el valor de p−value obtenido en el test de hipótesis es suficientemente bajo como para considerar significativas las diferencias observadas y por lo tanto rechazar H0. A menor valor de α, menor probabilidad de rechazar la hipótesis nula.
Por ejemplo, si se considera α=0.05, se rechazará la hipótesis nula en favor de la hipótesis alternativa si el p−value obtenido es menor que 0.05, y se tendrá una probabilidad del 5% de haber rechazado H0 cuando realmente es cierta.
En nivel de significancia debe establecerse en función de que error sea más costoso:
Error tipo I: Error de rechazar la H0 cuando realmente es cierta.
Error tipo II: Error de considerar como cierta H0 cuando realmente es falsa.
5. Condiciones para comparar dos medias independientes mediante t-test
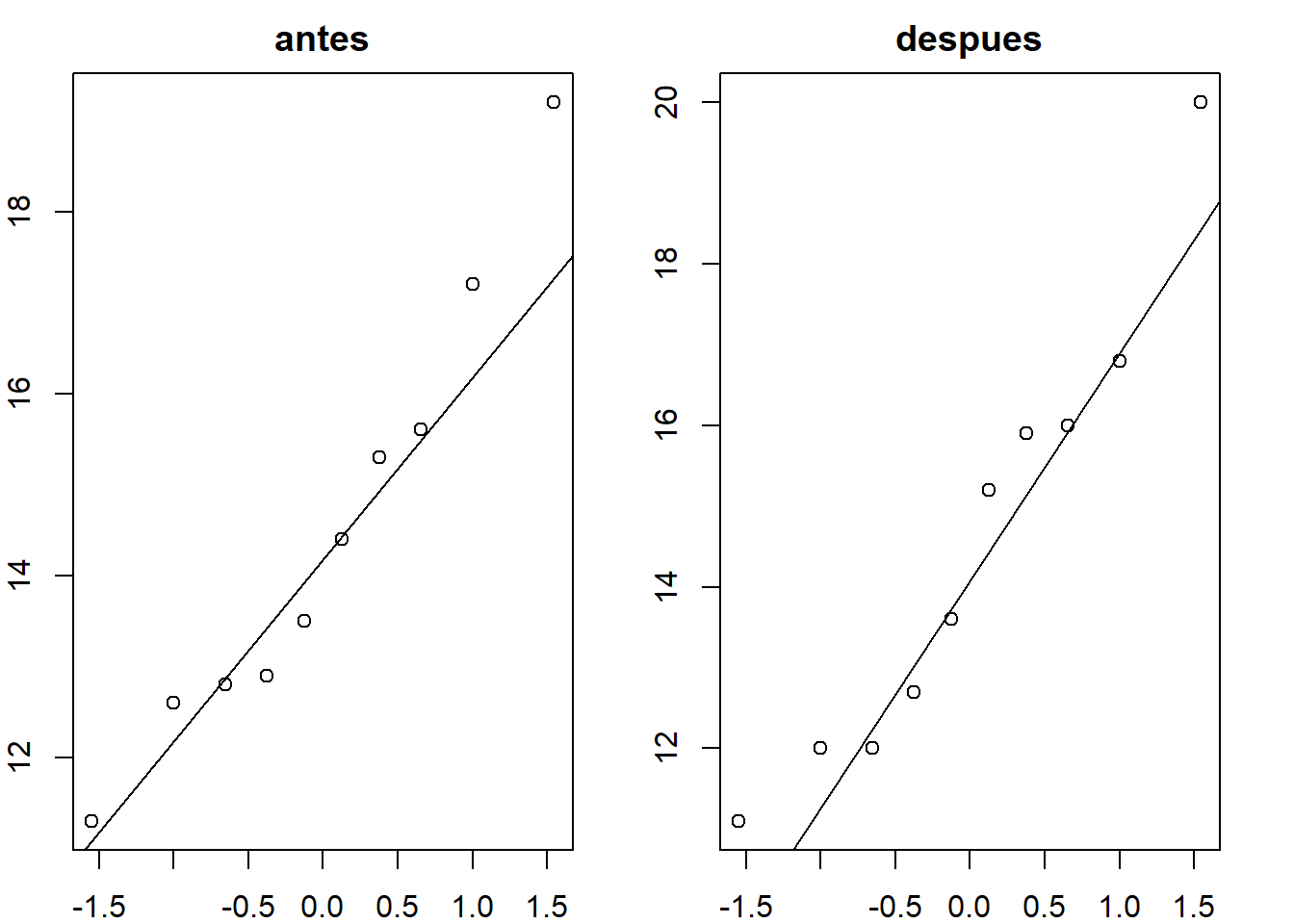
Método gráfico:
par(mar = c(2, 2, 2, 2))
par(mfrow = c(1, 2))
qqnorm(datos$antes, xlab = "", ylab = "", main = "antes")
qqline(datos$antes)
qqnorm(datos$despues, xlab = "", ylab = "", main = "despues")
qqline(datos$despues)
Método analítico:
shapiro.test(datos$antes)
Shapiro-Wilk normality test
data: datos$antes
W = 0.94444, p-value = 0.6033
shapiro.test(datos$despues)
Shapiro-Wilk normality test
data: datos$despues
W = 0.93638, p-value = 0.5135
Los gráficos qqnorm indican que las muestras se asemejan a los esperado en una población normal y los test de Saphiro−Wilk no muestran evidencias para descartar que las muestras procedan poblaciones sean normales (para un α de 0.05).
6. Cálculo de p-value
Parámetro estimado ˉd=mean( diferencia )=−0.05
grados de libertad =10−1=9
SE(promedio de las diferencias) =ˆSdiferencia √n=0.7412452√10=0.2344023
- Tcalc=ˉdSE=−0.050.2344023=−0.2133085
- p−value=P(tdf=9<−0.2133085)+P(tdf=9>0.2133085)
pt(q = -0.2133085, df = 9) + (1 - pt(q = 0.2133085, df = 9))
[1] 0.83584
7. Tamaño del efecto
En el caso particular de los t-test dependientes solo es posible aplicar la d de Choen.
d=∣ media de las diferencias ∣sd( diferencias )
8. Conclusión
En este caso, dado p−value >α, no hay evidencias significativas para rechazar H0 en favor de Ha. No se pude considerar que el rendimiento de los atletas haya cambiado.
Ejemplo II: Solución mediante R
R contiene la función t.test() que realiza un t.test con datos pareados si se le indica en el argumento. R calcula automáticamente las diferencias para cada evento, asumiendo que se las posiciones de cada vector se corresponden a los datos de un mismo individuo. Está función calcula además el intervalo de confianza para la diferencia de medias.
t.test(x = datos$antes, y = datos$despues, alternative = "two.sided",
mu = 0, paired = TRUE, conf.level = 0.95)
Paired t-test
data: datos$antes and datos$despues
t = -0.21331, df = 9, p-value = 0.8358
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-0.5802549 0.4802549
sample estimates:
mean of the differences
-0.05
library(effsize)
cohen.d(d = datos$antes, f = datos$despues, paired = TRUE)
Cohen's d
d estimate: -0.0169815 (negligible)
95 percent confidence interval:
lower upper
-0.1842481 0.1502851
Conclusión
En este caso, se ha demostrado como emplear el T-test para comparar medias poblacionales independientes.
De igual forma, se ha demostrado como emplear el T-test para comparar medias poblacionales dependientes (pareadas).
Referencias
- OpenIntro Statistics: Fourth Edition by David Diez, Mine Çetinkaya-Rundel, Christopher Barr libro
- Handbook of Biological Statistics by John H. McDonald
popular post

Problemas de transporte y asignación
Resumen: Existen dos tipos de problemas especiales en la investigación de operaciones, los problemas de transporte y de asignación.
Lire plus
Programación lineal
Resumen: Utilizar R para resolver problemas de programación lineal vinculados a la investigación de operaciones.
Lire plus
Programación lineal entera
Resumen: Utilizar R para resolver problemas de programación lineal entera vinculados a la investigación de operaciones.
Lire plus