Pruebas de Bartlett

¿Qué es la prueba de Bartlett?

En realidad, existen dos pruebas llamadas de Bartlett:

1. La primera es la prueba de homogeneidad de varianzas de Bartlett.
2. La segunda es la prueba de esfericidad de Bartlett (probar que la matriz de correlación tiene una matriz de identidad).

Prueba de Bartlett para homogeneidad de varianzas

En etse caso, la prueba de homogeneidad de varianzas de Bartlett se usa para probar que las varianzas son iguales para todas las muestras. Comprueba que la suposición de varianzas iguales sea cierta antes de ejecutar ciertas pruebas estadísticas como el ANOVA de una vía. Se usa cuando está bastante seguro de que los datos provienen de una distribución normal. Una prueba similar, llamada prueba de Levene, es una mejor opción para distribuciones no normales.

La hipótesis nula de la prueba es que las varianzas son iguales para todas las muestras. En términos estadísticos, eso es:

$$ H_{0}: \sigma_{1}^{2}=\sigma_{2}^{2}=\ldots=\sigma_{k}^{2} $$

La hipótesis alternativa (la que está probando) es que las varianzas no son iguales para un par o más:

$$ H_{0}: \sigma_{1}^{2} \neq \sigma_{2}^{2} \neq \ldots \neq \sigma_{k^{2}}{ }^{2} $$

Ejecución de la primera prueba de Bartlett

La fórmula para la prueba Bartlett es:

$$ \chi^{2}=\frac{(N-k) \ln (S_{p}^{2})-\sum_{i=1}^{k}(n_{i}-1) \ln (S_{i}^{2})}{1+\frac{1}{3(k-1)}(\sum_{i=1}^{k}(\frac{1}{n_{i}-1})-\frac{1}{N-k})} $$

Esta prueba no suele calcularse a mano (lo más probable es que desee usar software para la prueba), debido a la complejidad.

Prueba de Bartlett para la esfericidad

En este caso, la prueba de Bartlett para la esfericidad compara una matriz de correlación (una matriz de correlaciones de Pearson) con la matriz de identidad. En otras palabras, comprueba si hay redundancia entre variables que se pueden resumir con algunos factores.

Ejecución de la segunda prueba de Bartlett

El análisis de componentes principales (PCA) es una técnica de reducción de dimensiones. El objetivo es obtener un conjunto de factores que resuman, lo mejor posible, la información disponible en los datos. Los factores son combinaciones lineales de las variables originales (dicho enfoque solo puede manejar variables cuantitativas).

En este contexto, la prueba de esfericidad de Bartlett se utilizada para verificar la implementación de PCA en un conjunto de datos con un gran detalle.

Marco de datos y PCA en R

Se crea el marco de datos socio.data, el cual contiene \(n=12\) instancias y \(p=5\) variables (población, escuela, empleo, servicios, valor de la casa). Se usa el siguiente código R para cargar el conjunto de datos y realizar el análisis de componentes principales.

Se hace uso de la función data.frame para unir los 5 vectores (variables) y crear el marco de datos:

# Crear los vectores (variables)
Population	<- c(5700,	1000,	3400,	3800,	4000,	8200,	1200,	9100,	9900,	9600,	9600,	9400)
School	<- c(12.8,	10.9, 8.8,	13.6,	12.8,	8.3,	11.4, 11.5,	12.5,	13.7,	9.6,	11.4)
Employment <- c(2500,	600,	1000,	1700,	1600,	2600,	400,	3300,	3400,	3600,	3300,	4000)
Services	<- c(270,	10,	10,	140,	140,	60,	10,	60,	180,	390,	80,	100)
HouseValue	<- c(25000,	10000,	9000,	25000,	25000,	12000,	16000,	14000,	18000,	25000,	12000,	13000)

# Crear el marco de datos
socio.data <- data.frame(Population, School, Employment, Services, HouseValue)
print(socio.data)

   Population School Employment Services HouseValue
1        5700   12.8       2500      270      25000
2        1000   10.9        600       10      10000
3        3400    8.8       1000       10       9000
4        3800   13.6       1700      140      25000
5        4000   12.8       1600      140      25000
6        8200    8.3       2600       60      12000
7        1200   11.4        400       10      16000
8        9100   11.5       3300       60      14000
9        9900   12.5       3400      180      18000
10       9600   13.7       3600      390      25000
11       9600    9.6       3300       80      12000
12       9400   11.4       4000      100      13000

Ejecutar el PCA usando la función princomp:

socio.pca <- princomp(socio.data, cor = T)

Calcular la proporción de la varianza explicada de los factores:

parte.pca <- socio.pca$sdev^2/sum(socio.pca$sdev^2)*100
print(parte.pca)

    Comp.1     Comp.2     Comp.3     Comp.4     Comp.5 
57.4662719 35.9332019  4.2967377  1.9986811  0.3051075 

Calcular la proporción acumulada de la varianza explicada de los factores:

print(cumsum(parte.pca))

   Comp.1    Comp.2    Comp.3    Comp.4    Comp.5 
 57.46627  93.39947  97.69621  99.69489 100.00000 

Representación gráfica del PCA:

biplot(socio.pca)

Output

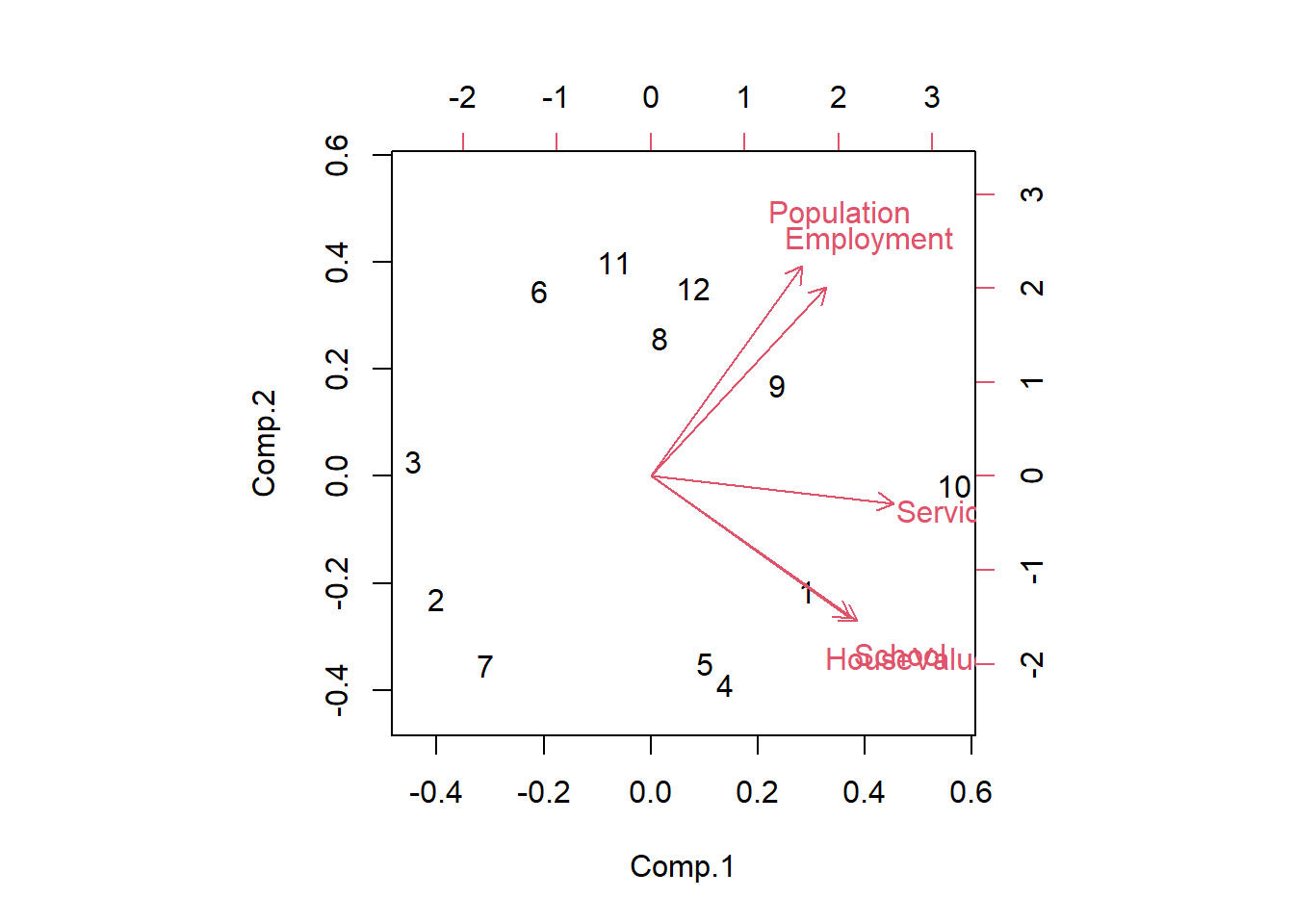
Los dos primeros factores representan el \(93.4\%\) de la varianza disponible. Se puede considerar que se teine una imagen precisa de la información disponible en los datos de estos factores.

Prueba de esfericidad de Bartlett en R

La prueba de Bartlett compara la matriz de correlación observada con la matriz de identidad. En otras palabras, comprueba si existe cierta redundancia entre las variables que se pueden resumir con unos pocos factores:

• Si las variables están perfectamente correlacionadas, solo un factor es suficiente.
• Si son ortogonales, se necesitan tantos factores como variables.

En este último caso, la matriz de correlación es la misma que la matriz identidad. Una estrategia simple es visualizar la matriz de correlación. Si los valores fuera de la diagonal principal suelen ser altos (en valor absoluto), algunas variables están correlacionadas; si la mayoría de estos valores están cerca de cero, el PCA no es realmente útil.

Cálculo de las correlaciones entre las variables

Calcular la matriz de correlación en R:

R <- cor(socio.data)
print(R)

           Population     School Employment  Services HouseValue
Population 1.00000000 0.00975059  0.9724483 0.4388708 0.02241157
School     0.00975059 1.00000000  0.1542838 0.6914082 0.86307009
Employment 0.97244826 0.15428378  1.0000000 0.5147184 0.12192599
Services   0.43887083 0.69140824  0.5147184 1.0000000 0.77765425
HouseValue 0.02241157 0.86307009  0.1219260 0.7776543 1.00000000

Algunas variables están correlacionadas (por ejemplo, población y empleo: \(0.97\) o escuela y valor de la vivienda: \(0.86\)). Aquí, el objetivo es solo obtener una impresión general sobre la redundancia entre las variables. Ahora bien, se debe confirmar con un riguroso procedimiento estadístico.

Prueba de esfericidad de Bartlett

La prueba de Bartlett comprueba si la matriz de correlación observada \(R=(r_{i j})_{(p \times p)}\) diverge significativamente de la matriz identidad (matriz teórica bajo \(H_{0}\): las variables son ortogonales). El PCA puede realizar una compresión de la información disponible solo si se rechaza la hipótesis nula.

Para medir la relación global entre las variables, se calcula el determinante de la matriz de correlación \(|R|\). Bajo \(H_{0}\), \(|R| = 1\); si las variables están altamente correlacionadas, se tiene \(|R| \approx 0\).

El estadístico de prueba de Bartlett indica en qué medida se desvía de la situación de referencia \(|R| = 1\), haciendo uso de la siguiente fórmula

$$ \chi^{2}=-(n-1-\frac{2 p+5}{6}) \times \ln |R| $$

Bajo \(H_{0}\), sigue una distribución \(\chi^{2}\) con un grado de libertad \([p \times(p-1) / 2]\).

Se realiza el cálculo en \(R\):

n <- nrow(socio.data)
p <- ncol(socio.data)
chi2 <- -(n-1-(2*p+5)/6)*log(det(R))
ddl <- p*(p-1)/2
print(chi2)

[1] 54.25167

print(ddl)

[1] 10

print(pchisq(chi2, ddl, lower.tail = F))

[1] 4.355652e-08

Se rechaza la hipótesis nula al nivel del \(5\%\) ($valor$ \(p = 4.35 \times 10^{-8} < 0.05\)). Por lo tanto, se puede realizar de manera eficiente un PCA en el conjunto de datos.

Nota:

La prueba de Bartlett tiene un gran inconveniente. Tiende a ser siempre estadísticamente significativo cuando aumenta el número de instancias \(n\).

Algunas referencias aconsejan utilizar esta prueba solo si la relación \(n:p\) (número de instancias dividido entre el número de variables) es inferior a \(5\).

Buscando en la web, encontré el paquete psych que calcula la prueba de esfericidad de Batlett con la función cortest.bartlett:

library(psych)
print(cortest.bartlett(R, n = nrow(socio.data)))

$chisq
[1] 54.25167

$p.value
[1] 4.355652e-08

$df
[1] 10

Conclusión

El test de esfericidad de Bartlett permite detectar si se puede o no resumir la información proporcionada por las variables iniciales en unos pocos factores. No obstante, no da indicaciones sobre el número apropiado de factores. En este contexto, he mostrado cómo calcularlos con un programa escrito en R. Finalmente, resulta importante mencionar que los cálculos son factibles solo si la matriz de correlación es invertible.

Referencias

• Esquivar, Y. (2008). La Enciclopedia Concisa de Estadística. Saltador.
• Larry, G. y Woollcott, S. (1993). The cartoon guide to statistics. New York: HarperPerennial.
• Klein, G. (2013). La caricatura: Introducción a la estadística. Colina y Wamg.
• Snedecor, George W. y Cochran, William G. (1989), Métodos estadísticos, octava edición, Iowa State University Press.
• Vogt, WP (2005). Diccionario de estadística y metodología: Una guía no técnica para las ciencias sociales. SABIO.